Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

a) Để \(A\in Z\) thì \(3⋮n-1\)
\(\Rightarrow n-1\in U\left(3\right)\)
Bảng:
| n-1 | -1 | -3 | 1 | 3 |
| n |
0 |
-2 | 2 | 4 |
Vậy...........
b) Để \(B\in Z\) thì \(x-2⋮x+3\)
\(\Rightarrow x+3-5⋮x+3\)
\(\Rightarrow-5⋮x+3\)
Bảng:
| x+3 | -1 | 5 | 1 | -5 |
| x | -4 | 2 | -2 | -8 |
Vậy...........

a.A: \(\dfrac{3}{x-1}\)
Để A nhận giá trị nguyên thì 3 chia hết x-1
Suy ra: x-1 thuộc Ư(3) ={1;-1;3;-3}
Ta có bảng sau:
| n-1 | -3 | -1 | 3 | 1 |
| n | -2 | 0 | 4 | 2 |
| Kết luận | Thỏa mãn | Thỏa mãn | Thỏa mãn | Thỏa mãn |
Vậy x thuộc { -2; 0;4 ;2}
a.Để \(A\in Z\) thì \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
Ta có:
\(x-1=1\\ x=1+1\\ x=2\\\)
\(x-1=-1\\ x=\left(-1\right)+1\\ x=0\)
\(x-1=3\\ x=3+1\\ x=4\)
\(x-1=-3\\ x=\left(-3\right)+1\\ x=-2\)
Vậy, để \(A\in Z\) thì \(x\in\left\{2;0;4;-2\right\}\)

Bài 2: a) \(\dfrac{x-3}{x+5}=\dfrac{5}{7}\)
\(\Leftrightarrow\left(x-3\right).7=\left(x+5\right).5\)
\(\Leftrightarrow7x-21=5x+25\)
\(\Leftrightarrow7x-5x=21+25\)
\(\Leftrightarrow2x=46\)
\(\Rightarrow x=46:2=23\)
b) \(\dfrac{7}{x-1}=\dfrac{x+1}{9}\)
\(\Leftrightarrow\left(x+1\right)\left(x-1\right)=63\)
\(\Leftrightarrow x^2-1=63\)
\(\Leftrightarrow x^2=64\)
\(\Rightarrow x^2=\left(\pm8\right)^2\)
\(\Rightarrow x=8\) hoặc \(x=-8\)
2)a) \(\dfrac{x-3}{x+5}=\dfrac{5}{7}\)
\(\Leftrightarrow7\left(x-3\right)=5\left(x+5\right)\)
\(7x-21=5x+25\)
\(7x-5x+25=21\)
\(2x+25=21\)
\(2x=-4\Rightarrow x=-2\)
b) \(\dfrac{7}{x-1}=\dfrac{x+1}{9}\)
\(7.9=\left(x+1\right)\left(x-1\right)\)
\(63=x\left(x-1\right)+1\left(x-1\right)\)
\(63=x^2-x+x-1\)
\(x^2=63+1=64\)
\(x=\left\{\pm8\right\}\)
c) \(\dfrac{x+4}{20}=\dfrac{2}{x+4}\)
\(\Leftrightarrow\left(x+4\right)\left(x+4\right)=2.20=40\)
\(x\left(x+4\right)+4\left(x+4\right)=40\)
\(x^2+4x+4x+16=40\)
\(x^2+8x=40-16=24\)
\(x\left(x+8\right)=24\)
\(x\in\left\{\varnothing\right\}\)
d) \(\dfrac{x-1}{x+2}=\dfrac{x-2}{x+3}\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)=\left(x-1\right)\left(x+3\right)\)
\(x\left(x-2\right)+2\left(x-2\right)=x\left(x+3\right)-1\left(x+3\right)\)
\(x^2-2x+2x-4=x^2+3x-x-3\)
\(\)\(x^2-4=x^2+2x-3\)
\(\Leftrightarrow x^2-x^2-2x+3=4\)
\(-2x+3=4\)
\(-2x=1\)
\(x=-\dfrac{1}{2}\)

a: \(\Leftrightarrow x\cdot\dfrac{62}{7}=\dfrac{29}{9}\cdot\dfrac{56}{3}=\dfrac{1624}{27}\)
hay \(x=\dfrac{1624}{27}:\dfrac{62}{7}=\dfrac{5684}{837}\)
b: \(\Leftrightarrow\dfrac{1}{5}:x=\dfrac{12}{35}\)
nên \(x=\dfrac{1}{5}:\dfrac{12}{35}=\dfrac{1}{5}\cdot\dfrac{35}{12}=\dfrac{7}{12}\)
c: \(\Leftrightarrow\left|2x+\dfrac{1}{3}\right|=\dfrac{30-7}{42}=\dfrac{23}{42}\)
=>2x+1/3=23/42 hoặc 2x+1/3=-23/42
=>2x=3/14 hoặc 2x=-37/42
=>x=3/28 hoặc x=-37/84

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 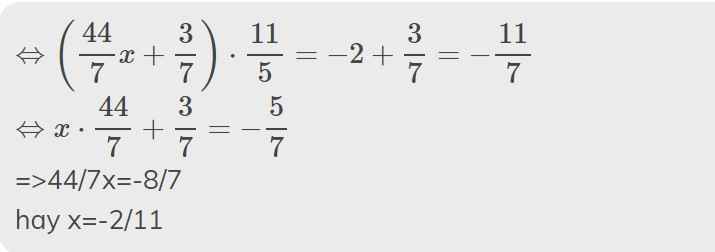
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

a) Để \(\dfrac{26}{x+3}\in N\) => \(26⋮\left(x+3\right)\) Hay \(\left(x+3\right)\inƯ\left(26\right)=\left\{1;2;13;26\right\}\)
Ta có bảng :
| x+3 | 1 | 2 | 13 | 26 |
| x | -2 | -1 | 10 | 23 |