Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử nhiệt độ cân bằng là t.
Nhiệt lượng do miếng nhôm toả ra là: \(Q_1=m_1.c_1(t_1-t)=0,5.880.(100-t)=440(100-t)\)
Nhiệt lượng do nước thu vào: \(Q_2=m_2.c_1(t-t_2)=0,8.4200.(t-20)=3360(t-20)\)
Phương trình cân bằng nhiệt ta có: \(Q_1=Q_2\)
\(\Rightarrow 440(100-t)=3360(t-20)\)
\(\Rightarrow t=29,26^0C\)
gọi m1,t1và c1lần lượt là khối lượng, nhiệt độ và nhiệt dung riêng của nhôm
m2,t2,c2 lần lượt là khối lượng , nhiệt độ và nhiệt dung riêng của nước
T là nhiệt độ cân bằng.
500g=0,5kg
800g=0,8kg
Theo đề bài ta có phương trinh cân bằng nhiệt:
m1.c1.(t1-T)=m2.c2.(T-t2)
<=> 0,5.880.(100-T)=0,8.4200.(T-20)
<=> 440.(100-T)=3360(T-20)
<=>44000-440T=3360T-67200
<=>-440T-3360T=-67200-44000
<=>-3800T=-111200
<=> T= \(\frac{-111200}{-3800}=29,26^o\)

a) Nhiệt độ của miếng nhôm ngay khi có cân bằng nhiệt là 27oC.
b) Nhiệt lượng do quả cầu tỏa ra
Q1 = m1C1(t1 –t) = 0,2.880.(100 – 27) = 12848J
c) Nhiệt lượng do nước thu vào để tăng nhiệt độ đến 27oC
Q2 = m2C2(t-t2) = m2.4200.(27-20) = \(29400.m_2\)
Áp dụng phương trình cân bằng nhiệt, ta có:
Q1 = Q2 => 12848= \(29400.m_2\)
m2 =\(\frac{12848}{29400}=0,44kg\)
Vậy khối lượng của nước là 0,44kg.

Nhiệt lượng nhôm tỏa ra:
\(Q_1=m_1c_1\left(t_1-t\right)=0,4\cdot880\cdot\left(120-50\right)=24640J\)
Gọi nhiệt độ ban đầu của nước là \(t_2^oC\)
Nhiệt lượng nước thu vào:
\(Q_2=m_2c_2\left(t-t_2\right)=2\cdot4200\cdot\left(50-t_2\right)\)
Cân bằng nhiệt: \(Q_1=Q_2\)
\(\Rightarrow24640=2\cdot4200\cdot\left(50-t_2\right)\)
\(\Rightarrow t_2=47,07^oC\)

Nl nhôm toả ra là
\(Q_{tỏa}=0,4.880\left(120-50\right)=24640J\)
Ta có pt cân bằng nhiệt
\(Q_{tỏa}=Q_{thu}\\ \Leftrightarrow24640=2.4200\left(50-t\right)\\ \Rightarrow t=47^o\)

ta có phương trình cân bằng nhiệt:
Qtỏa=Qthu
\(\Leftrightarrow Q=Q_1+Q_2\)
\(\Leftrightarrow Q=m_1C_1\left(t-t_1\right)+m_2C_2\left(t-t_2\right)\)
\(\Leftrightarrow Q=440\left(100-25\right)+8400\left(100-25\right)\)
\(\Rightarrow Q=663000J\)
2 lít = 2kg (nước)
gọi Q1 và Q2 lần lượt là nhiệt cần cung cấp để đun sôi nước và làm nóng ấm đến 1000C
Ta có
Q=Q1+Q2= m1.c1.Δt + m2.c2.Δt
= 2.4200.(100-25) + 0.5x880x(100-25)=663000(J)
vậy nhiệt lượng cần cung cấp để đun sôi ấm nước là: 663000(J)

a) Nhiệt lượng nc thu vào:
Qthu = m2 . c2 . Δ2 = 1 . 4200 . ( 30-25) = 21000J
b) Theo PT cân bằng nhiệt, ta có:
Qthu = Qtoả
⇒ Qtoả = 21000J
Mà: Qtoả = m1 . c1 . Δ1
⇒ 0,35 . 880 . (t1 - 30) = 21000
⇔ 308t1 - 9240 = 21000
⇔ 308t1 = 30240
⇔ t1 = \(\dfrac{30240}{308}\approx98,18\)độ C
bn kt lại xem

Tóm tắt:
Nhôm: m1 = 0,5kg
c1 = 880J/kg.K
Nước: m2 = 2kg
c2 = 4200J/kg.K
Đồng: m3 = 200g = 0,2kg
c3 = 380J/kg.K
t1 = 200C
t2 = 21,20C
t = ?
Giải:
Nhiệt độ của bếp lò = nhiệt độ ban dầu của thỏi đồng = t0C
Nhiệt lượng thau nhôm thu vào là:
Q1 = m1.c1.(t2 - t1)
Nhiệt lượng nước thu vào là:
Q2 = m2.c2.(t2 - t1)
Nhiệt lượng đồng tỏa ra là:
Q3 = m3.c3.(t - t2)
Theo PTCBN:
Q1 + Q2 = Q3
<=> m1.c1(t2 - t1) + m2.c2.(t2 - t1) = m3.c3.(t - t2)
<=> (t2 - t1).(m1.c1 + m2.c2) = m3.c3.(t - t2)
<=> (21,2 - 20).(0,5.880 + 2.4200) = 0,2.380.(t - 21,2)
<=> 10608 = 76.(t - 21,2)
<=> 139,58 = t - 21,2
<=> t = 160,780C
Nêu tiếp tục thả vào chậu nước một thỏi đá có khối lượng 100g ở 00C; Nước đá tan hết không? Tìm nhiệt độ cuối cùng của hệ thống hoặc lượng nước đá còn sót lại nếu không tan hết? Biết nhiệt lượng nóng chảy của nước đá \(\curlywedge\)=3,14.105 j/kg. Bỏ qua sự mất nhiệt ra ngoài môi trường
Giúp mk vs, mk đg cần gấp!!! Cảm ơn trước

Q(thu)=Q(tỏa)
<=> m2.c2.(t-t2)=m1.c1.(t1-t)
<=> 2.4200.(t-40)=0,4.880.(120-t)
<=>t=43,22oC
=> Nhiệt độ của nhôm và nước khi xảy ra CBN là khoảng 43,22oC
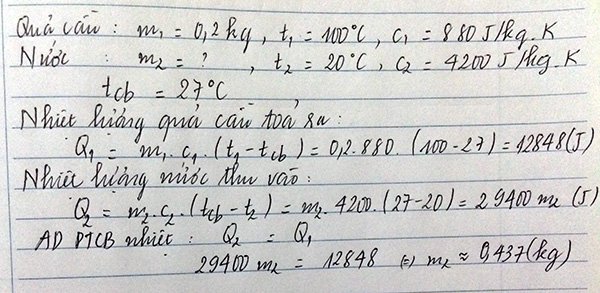
Tóm tắt:
\(t_1=100^oC\)
\(m_2=400g=0,4kg\)
\(t_2=20^oC\)
\(t=30^oC\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
==========
a) \(Q_2=?J\)
b) \(m_1=?kg\)
a) Nhiệt lượng nước thu vào:
\(Q_2=m_2.c_2.\left(t-t_2\right)=0,4.4200.\left(30-20\right)=16800J\)
b) Khối lượng của miếng nhôm là:
Theo phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1c_1.\left(t_1-t\right)=16800\)
\(\Leftrightarrow m_1=\dfrac{16800}{c_1.\left(t_1-t\right)}\)
\(\Leftrightarrow m_1=\dfrac{16800}{880.\left(100-30\right)}\approx0,27kg\)