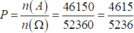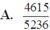Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A là biến cố: “có ít nhất một viên trúng vòng 10.”
⇒ A ¯ là biến cố: “Không viên nào trúng vòng 10.”
Gọi X là biến cố người thứ 1 bắn trúng vào10: P ( X ) = 0 , 75 ; P ( X ¯ ) = 1 − 0 , 75 = 0 , 25
Gọi Y là biến cố người thứ 2 bắn trúng vào10: P ( Y ) = 0 , 85 ; P ( Y ¯ ) = 1 − 0 , 85 = 0 , 15
Ta có; A ¯ = X ¯ . Y ¯ ; hai biến cố X ¯ ; Y ¯ là hai biến cố độc lập với nhau nên ta có:
P ( A ¯ ) = P ( X ¯ ) . P ( Y ¯ ) = 0 , 25. 0 , 15 = 0 , 0375
Do đó, xác suất của biến cố A là:
P ( A ) = 1 − P ( A ¯ ) = 1 − 0 , 0375 = 0 , 9625
Chọn đáp án A.

Gọi A là biến cố: “Lấy được ít nhất một viên bi xanh.”
Có tất cả 5 + 6=11 viên bi. Số phần tử của không gian mẫu là: Ω = C 11 2 = 55
- A là biến cố: “Không lấy được viên bi xanh nào.”
⇒ Ω A ¯ = C 6 2 = 15
Xác suất của biến cố A là: P ( A ¯ ) = 15 55 = 3 11
Xác suất của biến cố A là: P ( A ) = 1 − P ( A ¯ ) = 1 − 3 11 = 8 11
Chọn đáp án D.

Chọn A
Gọi A là biến cố “Đội tuyển Việt Nam và đội tuyển Malaysia được xếp trong cùng một bảng”.
Ta có: ![]() .
.
Do đó: 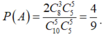 .
.

Đáp án D
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2 .
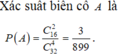

Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 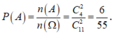 .
.

Đáp án C
Xếp ngẫu nhiên học sinh thành một hàng có 10! ⇒ n ( Ω ) = 10 !
Gọi biến cố A : “Xếp học sinh thành một hàng sao cho An và Bình đứng cạnh nhau”.
Xem An và Bình là nhóm X .
Xếp X và học sinh còn lại có 9! cách.
Hoán vị An và Bình trong X có 2! cách.
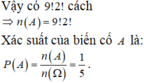

Số phần tử không gian mẫu:![]() .
.
(chọn 3 đỉnh bất kì từ 12 đỉnh của đa giác ta được một tam giác)
Gọi A: 3 đỉnh được chọn tạo thành tam giác đều ”.
(Chia 12 đỉnh thành 3 phần. Mỗi phần gồm 4 đỉnh liên tiếp nhau. Mỗi đỉnh của tam giác đều ứng với một phần ở trên.Chỉ cần chọn 1 đỉnh thì 2 đỉnh còn lại xác định là duy nhất).
Ta có: ![]() .
.
Khi đó: 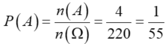 .
.
Chọn A.

Đáp án A
Số cách chọn 4 học sinh bất kì n ( Ω ) = C 35 4 = 52360 (cách).
Số cách chọn 4 học sinh chỉ có nam hoặc chỉ có nữ là C 20 4 + C 15 4 = 6210 (cách).
Do đó số cách chọn 4 học sinh có cả nam và nữ là n(A) = 52360 - 6210 = 46150 (cách).
Vậy xác suất cần tính là