Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=3x+m\)(*)
1) a) Đồ thị hàm số (*) đi qua \(A\left(-1,3\right)\)nên \(3=3.\left(-1\right)+m\Leftrightarrow m=6\).
b) Đồ thị hàm số (*) đi qua \(B\left(-2,5\right)\)nên \(5=3.\left(-2\right)+m\Leftrightarrow m=11\).
2) Đồ thị hàm số (*) cắt trục hoành tại điểm có hoành độ \(3x+m=0\Leftrightarrow x=-\frac{m}{3}\)
Suy ra \(-\frac{m}{3}=-3\Leftrightarrow m=9\).
3) Đồ thị hàm số (*) cắt trục tung tại điểm có tung độ \(y=3.0+m=m\)
suy ra \(m=-5\).

Hình tự vẽ nha
a) Vì A,B,D thuộc ( O; AD/2 )
\(\Rightarrow\widehat{ABD}=90^0\)
Vì \(EF\perp AD\Rightarrow\widehat{EFA}=90^0\)
Xét tứ giác ABEF có góc \(\widehat{ABE}=\widehat{AFE}=90^0\)
mà 2 góc này ở vị trí đối nhau trong tứ giác ABEF
\(\Rightarrow ABEF\)nội tiếp ( dhnb )
b) Vì A,C,D thuộc ( O; AD/2 )
\(\Rightarrow\widehat{ECD}=90^0\)
Xét tứ giác EFDC có: \(\widehat{ECD}=\widehat{EFD}=90^0\)
Mà 2 góc này ở vị trí đối nhau trong tứ giác EFDC
\(\Rightarrow EFDC\)nội tiếp
\(\Rightarrow\widehat{ECF}=\widehat{EDF}\)( cùng chắn cung EF )
Lại có: \(\widehat{BCA}=\widehat{BDA}\left(=\frac{1}{2}sđ\widebat{AB}\right)\)
\(\Rightarrow\widehat{BCA}=\widehat{ACF}\)
=> AC là phân giác góc BCF

\(P=\left(1+2a\right)\left(1+2bc\right)\le\left(1+2a\right)\left(1+b^2+c^2\right)=\left(1+2a\right)\left(2-a^2\right)\)
\(=\frac{3}{2}\left(\frac{2}{3}+\frac{4}{3}a\right)\left(2-a^2\right)\le\frac{3}{8}\left(\frac{8}{3}+\frac{4}{3}a-a^2\right)^2=\frac{3}{8}\left[\frac{28}{9}-\left(a-\frac{2}{3}\right)^2\right]^2\)
\(\le\frac{3}{8}.\left(\frac{28}{9}\right)^2=\frac{98}{27}\)
Dấu \(=\)khi \(\hept{\begin{cases}b=c\\\frac{2}{3}+\frac{4}{3}a=2-a^2,a-\frac{2}{3}=0\\a^2+b^2+c^2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{2}{3}\\b=c=\frac{\sqrt{\frac{5}{2}}}{3}\end{cases}}\).
Vậy \(maxP=\frac{98}{27}\).
Ta co : \(P=2a+2bc+2abc+1\)
Ap dung bdt Co-si : \(P\le a^2+b^2+c^2+2abc+2=2abc+3\)
Tiep tuc ap dung Co-si : \(1=a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}< =>\sqrt[3]{a^2b^2c^2}\le\frac{1}{3}\)
\(< =>a^2b^2c^2\le\frac{1}{27}< =>abc\le\frac{1}{\sqrt{27}}\)
Khi do : \(2abc+3\le2.\frac{1}{\sqrt{27}}+3=\frac{2}{\sqrt{27}}+3\)
Suy ra \(P\le a^2+b^2+c^2+2abc+2\le\frac{2}{\sqrt{27}}+3\)
Dau "=" xay ra khi va chi khi \(a=b=c=\frac{1}{\sqrt{3}}\)
Vay Max P = \(\frac{2}{\sqrt{27}}+3\)khi a = b = c = \(\frac{1}{\sqrt{3}}\)
p/s : khong biet dau = co dung k nua , minh lam bay do
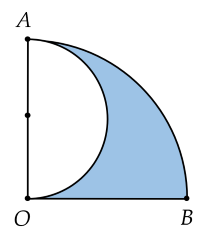
Diện tích phần tô màu là:
\(\dfrac{1}{4}.\pi.4^2-\dfrac{1}{2}.\pi.2^2=2\pi\left(cm^2\right)\)