Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại E và ΔDBA vuông tại A có
góc ABE chung
=>ΔABE đồng dạng với ΔDBA
=>BA/BD=BE/BA
=>BA^2=BD*BE
b: Xét ΔEDF vuông tại E và ΔEGB vuông tại E có
góc EDF=góc EGB
=>ΔEDF đồng dạng với ΔEGB
=>ED/EG=EF/EB
=>ED*EB=EG*EF
=>EG*EF=AE^2

a) BD, CE là các đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DA = DC; EA =EB
\(\Rightarrow\)ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)ED // BC; ED = 1/2 BC
\(\Delta GBC\)có MG = MB; NG = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta GBC\)
\(\Rightarrow\)MN // BC; MN = 1/2 BC
suy ra: MN // ED; MN = ED
\(\Rightarrow\)tứ giác MNDE là hình bình hành
c) MN = ED = 1/2 BC
\(\Rightarrow\)MN + ED = \(\frac{BC}{2}\)+ \(\frac{BC}{2}\)= BC

a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*

a) Vì tam giác ABC vuông tại A
=> BAC = 90 độ
=> Vì K là hình chiếu của H trên AB
=> HK vuông góc với AB
=> HKA = 90 độ
=> HKA = BAC = 90 độ
=> KH // AI
=> KHIA là hình thang
Mà I là hình chiếu của H trên AC
=> HIA = 90 độ
=> HIA = BAC = 90 độ
=> KHIA là hình thang cân
b) Vì KHIA là hình thang cân
=> KA = HI
= >KI = HA
Xét tam giác KAI vuông tại A và tam giác HIC vuông tại I có
KA = HI
KI = AH
=> Tam giác KAI = tam giác HIC ( cgv-ch)
=> KIA = ACB ( DPCM)
c) con ý này tớ nội dung chưa học đến thông cảm

A B C D M N E
a, xét tứ giác AMDN có :
góc BAC = góc DMA = góc AND = 90 (gt)
=> AMDN là hình chữ nhật (dấu hiệu)
b, AMDN là hình chữ nhật (câu a)
=> AN // DM hay AN // ME (1)
AMDN là hình chữ nhật => AN = MD (tc)
MD = ME do E đối xứng cới D qua M (gt)
=> AN = ME và (1)
=> AEMN là hình bình hành (dấu hiệu)
=> AN // ME (đn)
c, AMDN là hình chữ nhật (câu a)
để AMDN là hình vuông
<=> DN = DM (dh) (2)
có D là trung điểm của BC (gt)
DN // AB do AMDN là hình chữ nhật
=> DN là đường trung bình của tam giác ABC
=> DN = AB/2 (tc)
tương tự có DM = AC/2 và (2)
<=> AB/2 = AC/2
<=> AB = AC
tam giác ABC vuông tại A gt)
<=> tam giác ABC vuông cân tại A
vậy cần thêm đk tam giác ABC vuông để AMDN là hình vuông
+ vì AMDN là hình vuông
=> MN _|_ AD (tc)
=> S AMDN = NM.AD : 2 (Đl)
tam giác ABC vuông tại A có AD _|_ BC
=> S ABC = AD.BC : 2 (đl) (3)
BC = 2NM do NM là đường trung bình của tam giác ABC và (3)
=> S ABC = AD.2MN : 2
=> S ABC = 2S AMDN
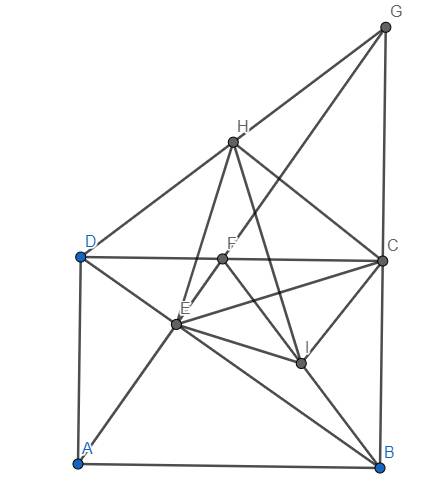
a) Ý 1: Dựa vào \(\widehat{AEB}=\widehat{DAB}=90^o\) và \(\widehat{ABD}\) chung, suy ra \(\Delta ABE~\Delta DBA\left(g.g\right)\)
Ý 2: Từ \(\Delta ABE~\Delta DBA\Rightarrow\dfrac{AB}{BD}=\dfrac{BE}{AB}\Rightarrow AB^2=BE.BD\)
b) Dễ thấy \(\widehat{DEF}=\widehat{BEG}=90^o\) và \(\widehat{DFE}=\widehat{EBG}\) (vì cùng phụ với \(\widehat{BDC}\)) nên suy ra \(\Delta EDF~\Delta EGB\left(g.g\right)\) \(\Rightarrow\dfrac{ED}{EG}=\dfrac{EF}{EB}\) \(\Rightarrow EG.EF=ED.EB\) (1)
Mặt khác, dễ dàng cm \(\Delta EAD~\Delta EBA\left(g.g\right)\) \(\Rightarrow\dfrac{EA}{EB}=\dfrac{ED}{EA}\) \(\Rightarrow EA^2=EB.ED\) (2)
Từ (1) và (2) \(\Rightarrow EA^2=EG.EF\left(=EB.ED\right)\)
c) Dễ thấy F là trực tâm của \(\Delta GBD\). \(\Delta GED\) vuông tại E có trung tuyến EH nên \(EH=\dfrac{1}{2}DG\). Tương tự suy ra \(CH=\dfrac{1}{2}DG\). Từ đó \(EH=DH\). Suy ra H nằm trên đường trung trực của đoạn CE (3)
Mặt khác, \(\Delta EBF\) vuông tại E có trung tuyến EI nên \(EI=\dfrac{1}{2}BF\). Tương tự, ta có \(CI=\dfrac{1}{2}BF\). Do đó \(EI=CI\) hay I nằm trên đường trung trực của đoạn CE (4)
Từ (3) và (4), suy ra HI là đường trung trực của đoạn CE, suy ra \(HI\perp CE\) (đpcm)
Hình vẽ đây nhé