Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

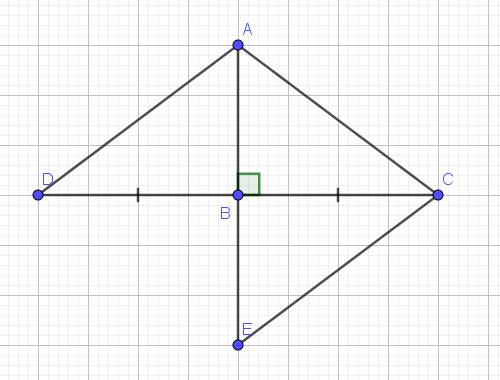
a) Xét hai tam giác vuông: \(\Delta ABD\) và \(\Delta ABC\) có:
AB chung
BD = BC (gt)
\(\Rightarrow\Delta ABD=\Delta ABC\) (hai cạnh góc vuông)
b) Do \(\Delta ABD=\Delta ABC\) (cmt)
\(\Rightarrow\widehat{ADB}=\widehat{ACB}\) (hai góc tương ứng)
Ta có: CE // AD (gt)
\(\Rightarrow\widehat{BCE}=\widehat{ADB}\) (so le trong)
\(\Rightarrow\widehat{BCE}=\widehat{ACB}\)
Xét hai tam giác vuông: \(\Delta CBA\) và \(\Delta CBE\) có:
BC là cạnh chung
\(\widehat{ACB}=\widehat{BCE}\) (cmt)
\(\Rightarrow\Delta CBA=\Delta CBE\) (cạnh góc vuông-góc nhọn kề)
\(\Rightarrow CA=CE\) (hai cạnh tương ứng)
\(\Delta ACE\) có CA = CE (cmt)
\(\Rightarrow\Delta ACE\) cân tại C

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
=>CB=CD
=>ΔCBD cân tại C
b: Ta có: \(\widehat{EAC}=\widehat{DCA}\)(hai góc so le trong, AE//CD)
\(\widehat{ECA}=\widehat{DCA}\)(ΔDCA=ΔBCA)
Do đó: \(\widehat{EAC}=\widehat{ECA}\)
=>ΔEAC cân tại E
c: Ta có: \(\widehat{EAC}+\widehat{EAB}=\widehat{BAC}=90^0\)
\(\widehat{ECA}+\widehat{EBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{EAC}=\widehat{ECA}\)
nên \(\widehat{EAB}=\widehat{EBA}\)
=>EA=EB
mà EA=EC(ΔEAC cân tại E)
nên EB=EC
=>E là trung điểm của BC
a) Do BD = BC và ∠BDA = ∠BCA = 90° nên ta có tam giác ABD = tam giác ABC (theo định lý góc - cạnh - góc).
=> Vậy, tam giác ABD = tam giác ABC.
b) Do CE // AD và AC cắt CE tại E nên ta có ∠CAE = ∠DAE.
- Do tam giác ABD = tam giác ABC nên AB = AD.
- Vì vậy, tam giác ADE là tam giác cân tại D, tức là AE = DE.
- Do tam giác ABD = tam giác ABC nên AC = BC.
- Vì vậy, tam giác BCE là tam giác cân tại B, tức là BE = CE.
- Do AE = DE và BE = CE nên AC = CE.
=> Vậy, ACE là tam giác cân.
a: Xét ΔABC vuông tại B và ΔABD vuông tại B có
AB chung
BC=BD
Do đó: ΔABC=ΔABD
b: Ta có: CE//AB
=>\(\widehat{CEA}=\widehat{DAB}\)
mà \(\widehat{DAB}=\widehat{CAB}\)(ΔABC=ΔABD)
nên \(\widehat{CAE}=\widehat{CEA}\)
=>ΔCAE cân tại C