Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
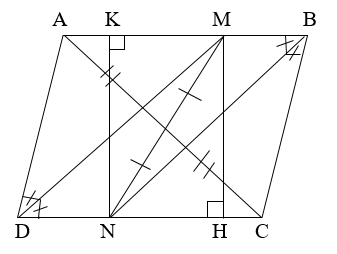
a) BD, CE là các đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DA = DC; EA =EB
\(\Rightarrow\)ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)ED // BC; ED = 1/2 BC
\(\Delta GBC\)có MG = MB; NG = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta GBC\)
\(\Rightarrow\)MN // BC; MN = 1/2 BC
suy ra: MN // ED; MN = ED
\(\Rightarrow\)tứ giác MNDE là hình bình hành
c) MN = ED = 1/2 BC
\(\Rightarrow\)MN + ED = \(\frac{BC}{2}\)+ \(\frac{BC}{2}\)= BC
a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*
a/
Ta có
\(AC\perp AB\Rightarrow AE\perp AB\)
\(DH\perp AB\)
=> AE // DH (1)
Ta có
\(AB\perp AC\Rightarrow AD\perp AC\)
\(HE\perp AC\)
=> AD // HE (2)
Từ (1) và (2) => ADHE là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{BAC}=90^o\)
=> ADHE là HCN (Hình bình hành có 1 góc vuông là HCN)
b/
Ta có
DH// AE (cmt) => DH // PE (1)
PE=AE (2)
DH=AE (cạnh đối HCN) (3)
Từ (2) và (3) => DH=PE (4)
Từ (1) và (4) => DHPE là hình bình hành (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)
c/
Xét tg AHC có
IA=IH (I là giao 2 đường chéo của hình chữ nhật ADHE)
MH=MC
=> IM là đường trung bình của tg AHC => IM//AC
Mà \(AC\perp AB\)
\(\Rightarrow IM\perp AB\)
Xét tg ABM có
\(AH\perp BC\Rightarrow AH\perp BM\)
\(IM\perp AB\left(cmt\right)\)
=> I là trực tâm của tg ABM (trong tam giác 3 đường cao đồng quy tại 1 điểm gọi là trực tâm của tam giác)
\(\Rightarrow BI\perp AM\left(dpcm\right)\)
a: Xét tứ giác ADCH có
M là trung điểm của AC
M là trung điểm của HD
Do đó: ADCH là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên ADCH là hình chữ nhật
b: Xét tứ giác ADHE có
HE//AD
HE=AD
Do đó:ADHE là hình bình hành