Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với hai số không âm a và b, bất đẳng thức Cô-si cho hai số đó là:
a + b 2 ≥ a b
Các hình chữ nhật có cùng diện tích thì ab không đổi. Từ bất đẳng thức a + b 2 ≥ a b và ab không đổi suy ra a + b 2 đạt giá trị nhỏ nhât bằng ab khi a = b.
Điều này cho thấy trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi bé nhất.

Với hai số không âm a và b, bất đẳng thức Cô-si cho hai số đó là:
a + b 2 ≥ a b
Các hình chữ nhật có cùng chu vi thì a + b 2 không đổi. Từ bất đẳng thức a + b 2 ≥ a b và không đổi suy ra ab đạt giá trị lớn nhất bằng a + b 2 khi a = b.
Điều này cho thấy trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Ta có bất đẳng thức Cauchy với 2 số a,b không âm :\(\frac{a+b}{2}\ge\sqrt{ab}\)
a)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->a+b=k không đổi
->Shcn=ab\(\le\frac{\left(a+b\right)^2}{4}\)=\(\frac{k^2}{4}\)
Dấu "=" xảy ra <=>a=b<=> hình vuông
b)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->ab=k không đổi
Chu Vi HCN=2(a+b)\(\ge\)\(4\sqrt{ab}\)=4\(\sqrt{k}\)
Dấu "=" xảy ra <=> a=b <=>Hình vuông

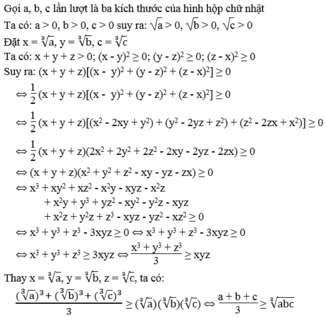
Vì a + b + c 3 ≥ a b c 3 và a + b + c 3 không đổi nên a + b + c 3 đạt giá trị nhỏ nhất ∛abc khi a = b = c.
Vậy trong các hình hộp chữ nhật có cùng thể tích thì hình lập phương có tổng ba kích thước bé nhất.

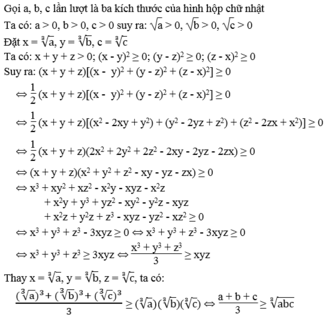
Các hình hộp chữ nhật có cùng tổng ba kích thước thì a + b + c 3 không đổi.
Vì a + b + c 3 ≥ a b c 3 và a + b + c 3 không đổi nên a b c 3 đạt giá trị lớn nhất a + b + c 3 khi a = b = c.
Vậy trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.

a) Gọi các kích thước hìh chữ nhật là x, y, z thỳ x, y, z > 0 vs x + y + z = k (ko đổi). Áp dụng bất đẳng thức Cô-si cho ba số dương ta có:
\(\sqrt[3]{xyz}\le\frac{x+y+z}{3}=\frac{k}{3}\)
Do đó: \(\text{V}=xyz\le\left(\frac{k}{3}\right)^3\)(ko đổi).
Vậy: V đạt giá trị lớn nhất khj và chỉ khi BĐT này trở thành đẳng thức hay là x = y = z, tức là khi hình chữ nhật trở thành hình lập phương.
b) Gọi 3 kích thước của hình hộp là x, y, z (ĐK)
Áp dụng bất đẳng thức Cô - si cho 3 số dương ta có :
\(x+y+z\ge3\sqrt[3]{xyz}\)
Từ đây ta có :
x + y + z nhỏ nhất là = \(3\sqrt[3]{xyz}\)
Bất đẳng thức Cô - si xảy ra dấu "=" khi : x = y = z.
Mọi người ko cần giúp mk nữa đâu vì mk làm được rùi nha !

Gọi hình chữ nhật là ABCD, nội tiếp đường tròn tâm O.
Vì tam giác ABC vuông tại B nên nội tiếp đường tròn đường kính AC, mà đường tròn đó chính là đường tròn tâm O ở trên
=> O là trung điểm AC.
Tương tự, O cũng là trung điểm BD.
b/ Chu vi lớn nhất.
Chu vi = 2(AB+BC) nên cần tìm giá trị AB+BC lớn nhất.
Mà ABC vuông tại B nên theo Pythagoras: \(AB^2+CB^2=AC^2=4R^2\)
Áp dụng bất đẳng thức \(\left(x-y\right)^2\ge0\Leftrightarrow\left(x+y\right)^2\le2\left(x^2+y^2\right)\Leftrightarrow x+y\le\sqrt{2\left(x^2+y^2\right)}\text{ }\left(x,y>0\right)\)
\(AB+BC\le\sqrt{2\left(AB^2+BC^2\right)}=\sqrt{8R^2}=2R\sqrt{2}=\text{không đổi.}\)
Dấu "=" xảy ra khi AB=BC <=> ABC vuông cân tại B <=> OB vuông góc AC <=> ABCD là hình vuông <=> ........ (bất cứ cái gí mình cần).
a/ Diện tích lớn nhất.
Tương tự như trên
\(S_{ABCD}=AB.BC\le\frac{AB^2+BC^2}{2}=2R^2\)
Dấu "=" xra khi AB=BC <=>....Hình vuông

