Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đầu bài ta có :
\(\begin{cases}u_2-u_1=7\\u_3-u_2=14\\u_4-u_3=21.......\\....u_n-u_{n-1}=7\left(n-1\right)\end{cases}\)
Cộng các vế của các phương trình của hệ, ta được :
\(\Leftrightarrow u_n-u_1=7+14+21+.....+7\left(n-1\right)=7\frac{n\left(n-1\right)}{2}\left(1\right)\)
Đặt \(u_n=35351\Rightarrow\left(1\right)\Leftrightarrow35351-1=7\frac{n\left(n-1\right)}{2}\)
\(\Leftrightarrow n^2-n-10100=0\rightarrow n=101\)
Do đó 35351 là số hạng thứ 101 của dãy số

Chọn C
Theo đề bài ta có:
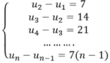
Cộng vế với vế các phương trình của hệ ta được:
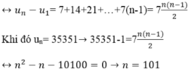

Theo đầu bài ta có : \(\cot\frac{A}{2}+\cot\frac{C}{2}=2\cot\frac{B}{2}\Leftrightarrow\frac{\sin\frac{A+C}{2}}{\sin\frac{A}{2}\sin\frac{C}{2}}=2\frac{\cos\frac{B}{2}}{\sin\frac{B}{2}}=2\frac{\sin\frac{A+C}{2}}{\cos\frac{A+C}{2}}\)
\(\Leftrightarrow\sin\left(\frac{A+C}{2}\right)\cos\left(\frac{A+C}{2}\right)=2\sin\frac{A}{2}\sin\frac{C}{2}\sin\frac{A+C}{2}=\left(\cos\frac{A-C}{2}-\cos\frac{A+C}{2}\right)\sin\frac{A+C}{2}\)
\(\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A+C}{2}=\cos\frac{A-C}{2}\sin\frac{A+C}{2}\)
\(\Leftrightarrow2\sin\left(A+C\right)=\frac{1}{2}\left(\sin A+\sin C\right)\)
\(\Leftrightarrow\sin A+\sin C=2\sin B\Rightarrow a+c=2b\)
Chứng tỏ 3 cạnh của tam giác lập thành cấp số cộng

Chọn đáp án B
Ta có: un = 4+ (n - 1).3 = 3n + 1,
1 ≤ n ≤ 100
vk = 1+ (k - 1).5 = 5k - 4,
1 ≤ k ≤ 100
Để một số là số hạng chung của hai cấp số cộng ta phải có:
3n +1 = 5k - 4 ⇔3n = 5(k-1)⇒ n ⋮ tức là n = 5t.
Khi đó; 3.5t = 5(k - 1) hay 3t = k - 1 nên k =1 + 3t, t ∈ Z
Vì 1 ≤ n ≤ 100 nên 1 ≤ t ≤ 20 . Mà t ∈ Z ⇒ t ∈ 1 ; 2 ; 3 ; . . . ; 19 ; 20
Ứng với 20 giá trị của t cho 20 giá trị của n và 20 giá trị của k.
Vậy có 20 số hạng chung của hai dãy

Ta có u n = 4 + ( n − 1 ) .3 = 3 n + 1 với 1 ≤ n ≤ 100
v k = 1 + ( k − 1 ) .5 = 5 k − 4 với 1 ≤ k ≤ 100
Để một số là số hạng chung của hai cấp số cộng ta phải có
3 n + 1 = 5 k − 4 ⇔ 3 n = 5 ( k − 1 )
⇒ n ⋮ 5 tức là n = 5 t với t ∈ ℤ
Vì 1 ≤ n ≤ 100 nên 1 ≤ t ≤ 20 . Do đó có 20 số hạng chung của hai dãy số.
Chọn đáp án B

Theo giả thiết ta có : \(\cot A+\cot C=2\cot B\)
\(\Leftrightarrow\frac{\sin\left(A+C\right)}{\sin A\sin C}=\frac{2\cos B}{\sin B}\)
\(\Leftrightarrow\sin^2B=2\sin B\sin C\cos B=\left[\cos\left(A-C\right)-\cos\left(A+C\right)\right]\cos B\)
\(\Leftrightarrow\sin^2B=\cos\left(A-C\right)\cos B-\cos\left(A+C\right)\cos B=-\cos\left(A-C\right)\cos\left(A+C\right)+\cos^2B\)
\(\Leftrightarrow\sin^2B=-\frac{1}{2}\left(\cos2A+\cos2C\right)+1-\sin^2B=-\frac{1}{2}\left(1-2\sin^2A+1-2\sin^2C\right)+1-\sin^2B\)
\(\Rightarrow2\sin^2B=\sin^2A+\sin^2C\Leftrightarrow2b^2=a^2+c^2\)
Vậy chứng tỏ \(a^2,b^2,c^2\) theo thứ tự đó cũng lập thành một cấp số cộng

Nếu 3 cạnh a, b, c lập thành cấp số cộng thì ta có a + c = 2b
\(\Leftrightarrow\sin A+\sin C=2\sin B\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A-C}{2}=4\sin\frac{B}{2}\cos\frac{B}{2}\left(1\right)\)
Vì \(A+C=180^0-B\Rightarrow\frac{A+C}{2}=90^0-\frac{B}{2}\)
<=> \(\sin\frac{A+C}{2}=\sin\left(90^0-\frac{B}{2}\right)=\cos\frac{B}{2}\) hoặc \(\cos\frac{A+C}{2}=\cos\left(90^0-\frac{B}{2}\right)=\sin\frac{B}{2}\) (*)
Do đó (1) trở thành :
\(\Leftrightarrow\sin\frac{A+C}{2}\cos\frac{A-C}{2}=2\sin\frac{A+C}{2}\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\sin\frac{B}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}+\sin\frac{A}{2}\sin\frac{C}{2}=2\cos\frac{A}{2}\cos\frac{C}{2}-2\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}=3\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cot\frac{A}{2}\cot\frac{C}{2}=3\) => Điều phải chứng minh

Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)