Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
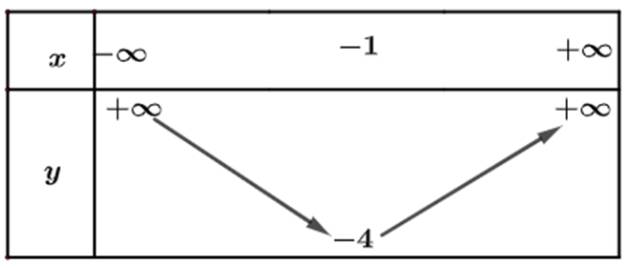
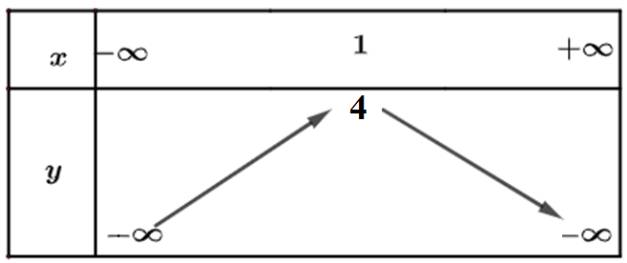
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3

Gọi x là số kilomet mà hành khách di chuyển \((x \ge 0)\)
a)
i) Khi đã lên taxi 4 chỗ, hành khách luôn phải trả 11 000 đồng dù đi hay không, do đó số tiền phải trả luôn bao gồm 11 000 đồng này.
Nếu \(0 \le x \le 0,5\), số tiền phải trả là 11 000 đồng
Nếu \(0,5 < x \le 30\) thì số tiền phải trả là \(11000 + 14500.(x - 0,5)\) hay \(3750 + 14500x\) (đồng).
Nếu \(x > 30\) thì số tiền phải trả là \(11000 + 14500.(30 - 0,5) + 11600.(x - 30)\) hay \(90750 + 11600x\) (đồng).
Vậy hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}11000\quad \quad \quad \quad \quad \quad \;0 \le x \le 0,5\quad \\3750 + 14500x\quad \quad \quad 0,5 < x \le 30\end{array}\\{90750 + 11600x\quad \quad \;x > 30}\end{array}} \right.\quad \)
ii)
Khi đã lên taxi 7 chỗ, hành khách luôn phải trả 11 000 đồng dù đi hay không, do đó số tiền phải trả luôn bao gồm 11 000 đồng này.
Nếu \(0 \le x \le 0,5\), số tiền phải trả là 11 000 đồng
Nếu \(0,5 < x \le 30\) thì số tiền phải trả là \(11000 + 15500.(x - 0,5)\) hay \(3250 + 15500x\) (đồng).
Nếu \(x > 30\) thì số tiền phải trả là \(11000 + 15500.(30 - 0,5) + 13600.(x - 30)\) hay \(60250 + 13600x\) (đồng).
Vậy hàm số \(g(x) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}11000\quad \quad \quad \quad \quad \quad \;0 \le x \le 0,5\quad \\3250 + 15500x\quad \quad \quad 0,5 < x \le 30\end{array}\\{60250 + 13600x\quad \quad \;x > 30}\end{array}} \right.\quad \)
b)
Nếu đặt toàn bộ xe 4 chỗ cho 30 hành khách thì cần 8 xe. Khi đó số tiền phải trả là:
\({f_1}(x) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}8.11000\quad \quad \quad \quad \quad \quad \;\;\;0 \le x \le 0,5\quad \\8.(3750 + 14500x)\quad \quad \quad 0,5 < x \le 30\end{array}\\{8.(90750 + 11600x)\;\quad \quad \;x > 30}\end{array}} \right.\quad \)
Nếu đặt toàn bộ xe 7 chỗ cho 30 hành khách thì cần 5 xe. Khi đó số tiền phải trả là:
\({g_1}(x) = \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}5.11000\quad \quad \quad \quad \;\;\quad \quad \;0 \le x \le 0,5\quad \\5.(3250 + 15500x)\quad \quad \quad 0,5 < x \le 30\end{array}\\{5.(60250 + 13600x)\quad \quad \;\;x > 30}\end{array}} \right.\quad \)
So sánh số tiền dựa theo số kilomet di chuyển:
+) Nếu \(0 \le x \le 0,5\)
\(\begin{array}{l}{f_1}(x) = 8.11000;\;{g_1}(x) = 5.11000\\ \Rightarrow {f_1}(x) > {g_1}(x)\end{array}\)
Vậy khi 30 người di chuyển quảng đường ít hơn hoặc bằng 0,5km thì đi xe 7 chỗ sẽ tốn ít tiền hơn.
+) Nếu \(0,5 < x \le 30\)
\(\begin{array}{l}{f_1}(x) = 8.(3750 + 14500x);\;{g_1}(x) = 5.(3250 + 15500x)\\ \Rightarrow {f_1}(x) - {g_1}(x) = 8.(3750 + 14500x) - 5.(3250 + 15500x)\\ = 13750 + 38500x\end{array}\)
Vì \(x > 0\) nên \({f_1}(x) - {g_1}(x) > 0\) hay \({f_1}(x) > {g_1}(x)\)
Vậy khi 30 người di chuyển quảng đường trên 0,5km đến 30km thì đi xe 7 chỗ sẽ tốn ít tiền hơn.
+) Nếu \(x > 30\)
\(\begin{array}{l}{f_1}(x) = 8.(90750 + 11600x);\;{g_1}(x) = 5.(60250 + 13600x)\\ \Rightarrow {f_1}(x) - {g_1}(x) = 8.(90750 + 11600x) - 5.(60250 + 13600x)\\ = 424750 + 24800x\end{array}\)
Vì \(x > 0\) nên \({f_1}(x) - {g_1}(x) > 0\) hay \({f_1}(x) > {g_1}(x)\)
Vậy khi 30 người di chuyển quảng đường trên 30km thì đi xe 7 chỗ sẽ tốn ít tiền hơn.
Kết luận: Nên đặt toàn bộ xe 7 chỗ thì có lợi hơn.

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

a ) \mathbb{R} \backslash (-3; \, 1]R\(−3;1]=(-∞;-3]∪(1;+∞)
b) (-\infty; \, 1) \backslash [-2; \, 0](−∞;1)\[−2;0]=(- (-\infty; \, 1) \backslash [-2; \, 0]∞;-2)∪(0;1)

Kết quả của mỗi lần thử là một cặp (i; j) với i và j lần lượt là số chấm xuất hiện trên hai xúc xắc, hai con xúc xắc gieo đồng thời nên không quan tâm thứ tự, ta có không gian mẫu là:
\(\Omega = \begin{array}{l}\{(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;2),(2;3),(2;4),(2;5),(2;6),(3;3),(3;4),(3;5),(3;6),\\(4;4),(4;5),(4;6),(5;5),(5;6),(6;6)\}\end{array} \)
Không gian mẫu gồm có 21 kết quả, tức là \(n\left( \Omega \right) = 21\)
a) Ta có tập hợp miêu tả biến cố A
\(A = \left\{ {(1;1),(2;2),(3;3),(4;4),(5;5),(6;6)} \right\} \Rightarrow n\left( A \right) = 6\)
Do đó, xác suất của biến cố A là: \(P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{21}} = \frac{2}{7}\)
b) Ta có tập hợp miêu tả biến cố B
\(B = \left\{ {(6;3),(5;4)} \right\} \Rightarrow n\left( B \right) = 2\)
Do đó, xác suất của biến cố B là: \(P\left( B \right) = \frac{{n(B)}}{{n(\Omega )}} = \frac{2}{{21}}\)

a) (-\infty ; \, 2) \cap (-1; \, +\infty)(−∞;2)∩(−1;+∞)=(-1;2)
b) (−1;6) ∪ [4;8)=(-1;8]
c) (−∞;−5] ∩(−5;1)={-5}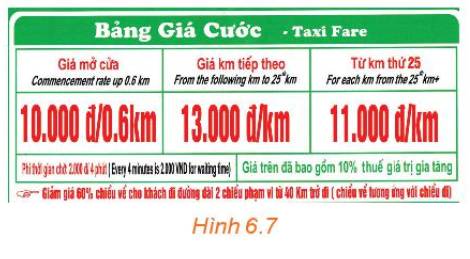

Gọi x là số km taxi đã đi; y (nghìn đồng) là số tiền cước phải trả
a) Khi di chuyển 25km thì
Với 0,6km đầu tiên, số tiền cước phải trả 10000 (đồng)
Với những km tiếp theo, số tiền cước phải trả 13000.(25-0,6)=317200(đồng)
Vậy số tiền cước phải trả 317200+10000=327200(đồng)
b) Khi hành khách đi từ 0km đến 0,6km thì \(y = 10\)(nghìn đồng)
Khi hành khách đi từ 0,7km đến 25km thì \(y = 10 + (x - 0,6).13 = 13x + 2,2\)(nghìn đồng)
Khi khách hàng đi từ 25km trở lên \(y = 13.25 + 2,2 + (x - 25).11 = 11x + 52,2\) (nghìn đồng)
c) Vẽ đồ thị hàm số
Nhìn trên đồ thị ta có thể thấy đồ thị đồng biến trên \(\left( {0; + \infty } \right)\)