Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các làm của bạn là đúng rồi nhé. Bài này bỏ giả thiết "trê đoạn AB đếm đc 42 vân sáng" thì mình vẫn tìm đc 6 vân ![]()
em ghi nhầm. em đếm ra 6 vân là đúng hay sai ạ. đáp án ghi tận 8 vân ạ.
theo cách đếm của em thì như thế này
* Xét bức xạ 1: goi C, D là 2 vân sáng gần AB nhất cách A, B 1 khoảng i1/2
suy ra CD = 9mm. n= CD/i1= 18 ( khoảng) suy ra có 19 vân sáng
suy ra AB có 18 vân sáng (do D không thuộc AB)
*tương tự với bức xạ 2 ta sẽ có 30 vân sáng thuộc AB
vậy số vân trùng là: 30 + 18 - 42 = 6 (vân)

Đáp án A
Tổng số vân sáng mà hai hệ vân cho được là 33 + 5 = 38
+ Số vân sáng của bức xạ λ 1 cho trên màn
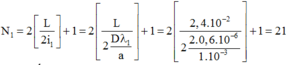
Vậy số vân sáng của bức xạ λ 2 trên màn sẽ là 38 – 21 = 17
→ Tại vị trí biên vân sáng bậc 10 của bức xạ λ 1 trùng với vân sáng bậc 8 của bức xạ λ 2
![]()


Các cặp trùng nhau trong đoạn A, B là (0, 0); (3, 4); (6, 8); (9, 12); (12, 16); (15, 20); (18, 24); (21, 28), (24, 32) với k1 < 24,25 ; k2 < 32,3.
→ Có 9 vân trùng của 2 hệ.
Đáp án B

Đáp án: 23 vị trí; 0,6mm.
Cách 1:
- Vân sáng của i1 trùng với vân tối của i2 →2i1 = 0,6mm; i2 = 0,4; i0 = 1,2mm;
- Ta có kM = -4,6; kN = 18,3. Số giá trị k bán nguyên là : 17,5 + 4,5 + 1 = 23 giá trị.
Cách 2:
+ Vân sáng của λ1 trùng với vân sáng của λ2: \(\frac{k_1}{k_2}=\frac{i_1}{i_2}=\frac{4}{3}\)
\(\Rightarrow\) Vân sáng có tọa độ 4ki1 của λ1 trùng với vân sáng có tọa độ 3ki2của λ2
\(\Rightarrow\) Vân sáng có tọa độ 2ki1 của λ1 trùng với vân sáng có tọa độ 1,5 ki2của λ2 (k lẻ)
\(\Rightarrow\) xtrùng = \((k+\frac{1}{2})4i_1(mm) \Rightarrow 5,5\leq(k+\frac{1}{2})4i_1\leq 2,2.10\)
\(\Leftrightarrow{-5,08}\leq{k}\leq{17,8}\)
\(\Rightarrow\) có 23 vị trí thỏa mãn.
Khoảng cách gần nhất từ điểm thỏa mãn đến vân trung tâm tương ứng với k = 0
xmin = 0,5.4i1 = 0,6 (mm)





Bạn tham khảo bài tương tự này nhé
Câu hỏi của nguyễn mạnh tuấn - Học và thi online với HOC24