Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) M là trung điểm AC(gt) => AM=CM
Xét tg BMC và tg DMA ta có:
- BM=DM(gt)
- ^BMC=^DMA(đối đỉnh)
- MC=MA(cmt)
=> tg BMC=tg DMA(c.g.c)
b) tg BMC=tg DMA(câu a)
=> ^MBC=^MDA (2 góc tương ứng)
Mà 2 góc này so le trong => AD//BC
Lại có: AH vuông góc BC(gt)
=> AH vuông góc AD (quan hệ //, vuông góc)
c) Ta có: AH vuông góc AD( câu b)
CK vuông góc AD(gt)
=> AH//CK(1)
Mà AD//BC(câu b) hay AK//CH (2)
Từ (1),(2) => AH=CK; AK=CH(3)
Tg BMC= tg DMA (câu a) => BC=DA(4)
Lại có: BC=CH + BH(5)
DA= AK + DK(6)
Từ (3)(4)(5)(6) => BH=DK
Có: ^MBC=^MDA(câu b) hay ^MBH=^MDK
Xét tg BMH và tg DMK có:
- BM=DM(gt)
- ^MBH=^MDK (cmt)
- BH=DK (cmt)
=> tg BMH=tg DMK (c.g.c)
=> ^BMH=^DMK
=>^BMH + ^BMK =^DMK+^BMK
Hay: ^HMK=^BMD=180°
=> H, M, K thẳng hàng

HÌnh bạn tự vẽ ra giấy nháp nhé
Dễ dàng tính được bc = 13
Áp dụng hệ thức lượng giác trong tam giác => AB^2 = BH. BC
Giải ra được BH = 25/13
Rồi sau đó tính được CH
Sau đó áp dụng định lí Pitago vào các tam giác vuông ABH và AHC để tính Ah và HK
Bạn có thể giải ra chi tiết được ko? Mình chưa học hệ thứ lượng giác nên bạn giải cách khác cho mình nhé.
Cảm ơn bạn rất nhiều.

a, Ta có ∆ABC cân ở A(gt)
AH\(\perp\) BC=>AH là đường cao
(1)=>AH đồng thời là trung tuyến=>HB=HC
(2)=>AH đồng thời là phân giác=>góc BAH=góc CAH
b, Áp dụng định lí pyta go cho ∆ABH ta có
AB2=AH2+BH2 =>52=42+HB2=>HB=√52--42=3
d, Xét ∆DHB và ∆EHC có
Góc HDB=góc HEC =90°(HD\(\perp\) AB, HE vuông góc ACgt)
Góc B=góc C ( tam giác ABC cân tai A gt)
HB =HC (cmt)
=> ∆DHB=∆EHC(ch-cgv)=>HD=HE=>∆HDE cân tại H

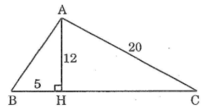
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

b
AH vuông góc với BC
BC song song với EK
=>AH vuông góc với EK
c: HK=9,6(cm)