Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
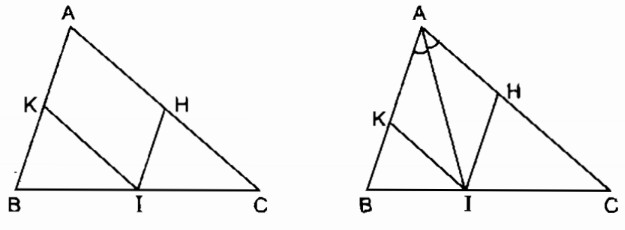
a. Ta có: IK // AC (gt)
hay IK // AH
IH // AB (gt)
hay IH // AK
Vậy tứ giác AHIK là hình bình hành (theo định nghĩa)
b. Hình bình hành AHIK là hình thoi nên đường chéo AI là phân giác của
Ngược lại AI là phân giác của . Hình bình hành AHIK có đường chéo là phân giác của một góc nên hình bình hành AHIK là hình thoi.
Vậy nếu I là giao điểm của đường phân giác của với cạnh BC thì tứ giác AHIK là hình thoi.
c. Hình bình hành AHIK là hình chữ nhật
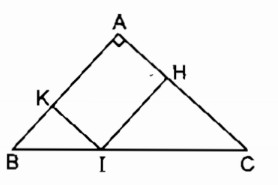
⇒ˆA=900⇒A^=900suy ra ∆ ABC vuông tại A
Ngược lại ∆ ABC có ˆA=900A^=900
Suy ra: Hình bình hành AHIK là hình chữ nhật.
Vậy nếu ∆ ABC vuông tại A thì tứ giác AHIK là hình chữ nhật.

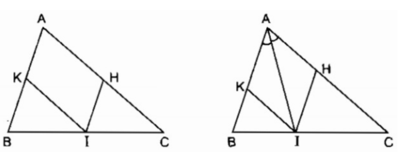
Hình bình hành AHIK là hình chữ nhật
⇒ ∠ A = 90 0 suy ra ∆ ABC vuông tại A. Ngược lại ΔABC có ∠ A = 90 0
Suy ra hình bình hành AHIK là hình chữ nhật
Vậy nếu ∆ ABC vuông tại A thì tứ giác AHIK là hình chữ nhật.

a: Xéttứ giác APDQ có
AP//DQ
AQ//DP
Do đó: APDQ là hình bình hành
b: C=(AP+AQ)*2=5*2=10cm
c: Vì APDQ là hình bình hành
nên AD cắt PQ tại trung điểm của mỗi đừog
=>P đối xứng với Q qua I

a) Xét tứ giác AQMP có
PM//AQ(PM//AC, Q∈AC)
QM//AP(QM//AB, P∈AB)
Do đó: AQMP là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A