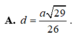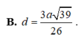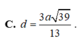Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

z C B O A D y S x M N
a. Do ABCD là hình thoi có tâm là O nên từ giả thiết ta có :
\(C=\left(-2;0;0\right)\)
\(D=\left(0;-1;0\right)\)
Từ đó M là trung điểm của SC nên :
\(M\left(-1;0=-\sqrt{2}\right)\)
Ta có \(\overrightarrow{SA}=\left(2;0;-2\sqrt{2}\right)\)
\(\overrightarrow{BM}=\left(-1;-1;\sqrt{2}\right)\)
Gọi \(\alpha\) là góc giữa 2 đường thẳng SA, MB, ta có :
\(\cos\alpha=\frac{\left|\overrightarrow{SA.}\overrightarrow{BM}\right|}{\left|\overrightarrow{SA}\right|.\left|\overrightarrow{MB}\right|}=\frac{\left|-2-4\right|}{\sqrt{4+8}.\sqrt{1+2+1}}=\frac{6}{4\sqrt{3}}=\frac{\sqrt{3}}{2}\)
Vậy \(\alpha=60^0\)
Để tính khoảng cách giữa 2 đường thẳng chéo nhau SA, BM ta sử dụng công thức :
\(d\left(SA;BM\right)=\frac{\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{AB}\right|}{\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right]\right|}\) (1)
Theo công thức xác định tọa độ vecto \(\left[\overrightarrow{SA};\overrightarrow{BM}\right]\) ta có :
\(\left[\overrightarrow{SA};\overrightarrow{BM}\right]=\left(\left|\begin{matrix}0&-2\sqrt{2}\\-1&\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&2\\\sqrt{2}&-1\end{matrix}\right|;\left|\begin{matrix}2&0\\-1&-1\end{matrix}\right|\right)\)
\(=\left(-2\sqrt{2};1;0\right)\)
\(\Rightarrow\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right]\right|=\sqrt{12}\)
\(\overrightarrow{AB}=\left(-2;1;0\right)\)
\(\Rightarrow\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{AB}=4\sqrt{2}\)
Thay vào (1) ta có :
\(d\left(SA;BM\right)=\frac{4\sqrt{2}}{\sqrt{12}}=\frac{2\sqrt{6}}{3}\)
b. Vì AB \\ mặt phẳng (SDC) nên MN \\ DC. Suy ra N là trung điểm của SD
\(\Rightarrow N=\left(0;-\frac{1}{2};\sqrt{2}\right)\)
Dễ thấy :
\(V_{S.ABMN}=V_{S.ABN}+V_{S.BMN}\)
\(=\frac{1}{6}\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{SN}\right|+\frac{1}{6}\left|\left[\overrightarrow{SB};\overrightarrow{SM}\right].\overrightarrow{SN}\right|\) (2)
Ta có \(\overrightarrow{SA}=\left(2;0;-2\sqrt{2}\right)\)
\(\overrightarrow{SN}=\left(0;-\frac{1}{2};-\sqrt{2}\right)\)
\(\overrightarrow{SB}=\left(0;1;-2\sqrt{2}\right)\)
\(\overrightarrow{SM}=\left(-1;0;-\sqrt{2}\right)\)
Ta lại có :
\(\left[\overrightarrow{SA};\overrightarrow{SB}\right]=\left(\left|\begin{matrix}0&-2\sqrt{2}\\-1&-2\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&2\\-2\sqrt{2}&0\end{matrix}\right|;\left|\begin{matrix}2&0\\0&1\end{matrix}\right|\right)\)
\(=\left(2\sqrt{2};4\sqrt{2};2\right)\)
\(\left[\overrightarrow{SB};\overrightarrow{SM}\right]=\left(\left|\begin{matrix}1&-2\sqrt{2}\\0&\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&0\\-\sqrt{2}&-1\end{matrix}\right|;\left|\begin{matrix}0&1\\-1&0\end{matrix}\right|\right)\)
\(=\left(-\sqrt{2};2\sqrt{2};1\right)\)
Thay vào (2) được :
\(V_{S.ABMN}=\frac{1}{6}\left(\left|-2\sqrt{2}-2\sqrt{2}\right|+\left|-\sqrt{2}-\sqrt{2}\right|\right)=\sqrt{2}\)

I K H B A D C
Giả sử : \(\widehat{B}=45^o\) (trường hợp khác \(\widehat{B}=135^o\) )
ta có : \(\begin{cases}IA=IB\\DA=DB\end{cases}\) \(\Rightarrow ID\perp AB\)
\(\overrightarrow{ID}=\left(-2;1\right)\) ptdt ID nhận \(\overrightarrow{n_{ID}}=\left(1;2\right)\) làm VTPT ta có pt: \(x+2y+3=0\)
ptdt AB đi qua K và nhận \(\overrightarrow{ID}\) làm VTPT ta có pt : \(-2x+y+9=0\)
tọa độ trung điểm H của AB là nghiệm của hệ : \(\begin{cases}x+2y=-3\\-2x+y=-9\end{cases}\) \(\Rightarrow\begin{cases}x=3\\y=-3\end{cases}\) vậy \(H\left(3;-3\right)\)
pt đường tròn tâm H bán kính \(HD=\sqrt{4+16}=\sqrt{20}\) là : \(\left(x-3\right)^2+\left(y+3\right)^2=20\)
Tọa độ của A và B là nghiệm của hệ : \(\begin{cases}-2x+y=-9\\\left(x-3\right)^2+\left(y+3\right)^2=20\end{cases}\) giải nghiệm ta được \(\begin{cases}x=5\\y=1\end{cases}\) hoặc \(\begin{cases}x=1\\y=-7\end{cases}\) vì A có tung độ dương nên \(A\left(5;1\right);B\left(1;-7\right)\)
C là giao điểm của dt BD và IC:
ptdt BD nhận \(\overrightarrow{n}=\left(6;2\right)=2\left(3;1\right)\) làm VTPT nên ta có pt : \(3x+y=-4\)
ptdt IC nhận \(\overrightarrow{n}=\left(4;3\right)\) làm VTPT nên ta có pt : \(4x+3y=-2\)
vậy tọa độ C là nghiệm của hệ :\(\begin{cases}3x+y=-4\\4x+3y=-2\end{cases}\) \(\Leftrightarrow\begin{cases}x=-2\\y=2\end{cases}\) vậy \(C\left(-2;2\right)\)

Ta có \(\left(SHC\right)\cap\left(SHD\right)=SH\)
Từ giả thiết \(\left(SHC\right)\perp\left(ABCD\right);\left(SHD\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(\Leftrightarrow V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}AB.AD.SH=\frac{1}{3}a^2\sqrt{3}.SH\left(1\right)\)
Ta có \(SH\perp\left(ABCD\right)\Rightarrow HD\) là hình chiếu của SD trên (ABCD), suy ra góc giữa SD và (ABCD) là \(\widehat{SDH}=60^0\Rightarrow SH=HD\tan\widehat{SDHH}=\frac{a\sqrt{39}}{2}\)
Khi đó \(V_{S.ABCD}=\frac{1}{2}a^3\sqrt{13}\)
Dựng hình bình hành ACBE. Khi đó AC//BE suy ra AC//(SBE)
\(\Rightarrow d\left(AC,SB\right)=d\left(AC,\left(SBE\right)\right)=d\left(A,\left(SBE\right)\right)=2d\left(H,\left(SBE\right)\right)\)
Gọi K, I lần lượt là hình chiếu của H trên BE và SK.
Khi đó \(BE\perp KH,BE\perp SH\Rightarrow BE\perp HI\left(1\right)\)
Mặt khác \(HI\perp SK\left(2\right)\)
Từ (1) và (2) suy ra \(HI\perp\left(SBE\right)\Rightarrow d\left(H,\left(SBE\right)\right)=HI\)
Tính được \(HK=\frac{a\sqrt{3}}{4};HI=\frac{a\sqrt{39}}{\sqrt{212}}\)
\(\Rightarrow d\left(AC,SB\right)=2d\left(H,\left(SBE\right)\right)=2HI=\frac{a\sqrt{39}}{\sqrt{53}}=\frac{a\sqrt{2067}}{53}\)

A H B C A' B' C' K I
Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)