
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(\frac{a}{c}=\frac{b}{d}\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)
\(\Leftrightarrow\frac{a^2}{b^2}=\frac{ac}{bd}=\frac{4a^2}{4b^2}=\frac{6ac}{6bd}=\frac{4a^2-6ac}{4b^2-6bd}=\frac{4a^2+6ac}{4b^2+6bd}\)(Áp dụng tính chất dãy tỉ số bàng nhau)
\(\Leftrightarrow\left(4a^2-6ac\right)\left(4b^2+6bd\right)=\left(4a^2+6ac\right)\left(4b^2-6bd\right)\)(Nhân chéo)
Chúc bạn học tốt!

2 . seafood
3 . bulid sandcastle
4 . fireman
5 . brush the teeth
6 . basketball
7 . apple
1 . sit down
2 . seafood
3 . sand castle
4 . annoyed
5 . toothpaste
6 .basketball
7 . delicate
8 . honey

A B C D M E F
Giải:
a, Xét \(\Delta ABM,\Delta DCM\) có:
AM = MD ( gt )
\(\widehat{AMB}=\widehat{DMC}\) ( đối đỉnh )
BM = MC ( gt )
\(\Rightarrow\Delta ABM=\Delta DCM\left(c-g-c\right)\left(đpcm\right)\)
b, Vì \(\Delta ABM=\Delta DCM\Rightarrow\widehat{ABM}=\widehat{DCM}\) ( góc t/ứng )
\(\Rightarrow\)AB // CD ( đpcm )
c, Xét \(\Delta BEM,\Delta CFM\) có:
BM = CM ( gt )
\(\widehat{BEM}=\widehat{CFM}=90^o\)
\(\widehat{EMB}=\widehat{FMC}\) ( đối đỉnh )
\(\Rightarrow\Delta BEM=\Delta CFM\) ( c.huyền - g.nhọn )
\(\Rightarrow EM=FM\) ( cạnh t/ứng )
\(\Rightarrow M\) là trung điểm của EF ( đpcm )
Vậy...
Ta có hình vẽ:
M A B C D E F
a/ Xét tam giác ABM và tam giác DCM có:
AM = MD (GT)
AMB = DMC (đđ)
BM = MC (M là trung điểm BC)
Vậy tam giác ABM = tam giác DCM
b/ Ta có: tam giác ABM = tam giác DCM (cmt ở câu a)
=> góc BAM = góc MDC (hai góc tương ứng)
Mà hai góc này đang ở vị trí so le trong
=> AB // DC (đpcm)
c/ Xét hai tam giác vuông BEM và CFM có:
BM = MC (M là trung điểm BC)
EMB = FMC (đđ)
Vậy tam giác BEM = tam giác CFM
=> ME = MF (1)
Ta có: góc EMB = góc FMC (đđ)
Mà góc EMB + góc EMC = 1800 (kề bù)
=> góc FMC + góc EMC = 1800
=> góc EMF = 1800
Vậy E;M;F thẳng hàng (2)
Từ (1) và (2) => M là trung điểm EF

Bài 1: Chọn câu đúng. Nếu thì:
A. a = c
B. a.c = b.d
C. a.d = b.c
D. b = d
Lời giải:
Ta có: Nếu thì a.d = b.c
Đáp án cần chọn là: C
Bài 2: Chọn câu sai. Nếu a.d = b.c và a, b, c, d ≠ 0 thì:
Lời giải:
Nếu a.d = b.c và a, b, c, d ≠ 0 thì ta có∶
nên A, B, D đúng, C sai
Đáp án cần chọn là: C
Bài 3: Chỉ ra đáp án sai: Từ tỉ lệ thức ta có tỉ lệ thức sau:
Lời giải:
Ta có ở đáp án C: 35.5 ≠ 63.9 do đó
Đáp án cần chọn là: C
Bài 4: Chỉ ra đáp án sai: Từ tỉ lệ thức ta có tỉ lệ thức sau:
Lời giải:
Vậy A, B, D đúng, C sai
Đáp án cần chọn là: C
HT

Kẻ thêm tia Cz // Ax // By
Ta có góc C1 +130 = 180 ( TCP do Ax//Cz)
góc C1 = 180 -130 =50 độ
=> C2 = 90 - 50 = 40 độ
Ta có C2 + CBy = 180 ( TCP do Cz // By)
40 + CBy = 180 độ
CBy = 180 -40 =140 độ
CBy = 180 độ nha bạn

1.Kết quả phép tính36.34.32 là:
A.272 B.312 C.348 D.30
2.Từ tỉ lệ thức \(\frac{a}{b}\)=\(\frac{c}{d}\)(a,b,c,d #0) ta có thể suy ra:
A.\(\frac{d}{b}\)=\(\frac{c}{a}\) B.\(\frac{a}{b}\)=\(\frac{c}{d}\)
C.\(\frac{a}{c}\)=\(\frac{d}{b}\) D.\(\frac{a}{d}\)=\(\frac{b}{c}\)
3.Nếu\(\sqrt{x}\)=4 thì x bằng:
A.\(\pm\)2 B.\(\pm\)6 C.\(\pm\)2 D.\(\pm\)16
Hok tốt!

\(\left|x-y\right|\ge\left|x\right|-\left|y\right|\)
\(\Leftrightarrow\left(x-y\right)^2\ge\left(\left|x\right|-\left|y\right|\right)^2\)
\(\Leftrightarrow x^2-2xy+y^2\ge x^2+y^2-2.\left|x\right|.\left|y\right|\)
\(\Leftrightarrow xy\le\left|x\right|.\left|y\right|\) (luôn đúng)
Ta có đpcm










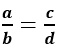 thì:
thì: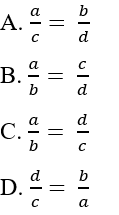
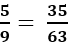 ta có tỉ lệ thức sau:
ta có tỉ lệ thức sau: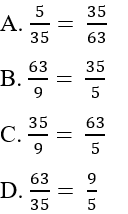
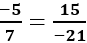 ta có tỉ lệ thức sau:
ta có tỉ lệ thức sau: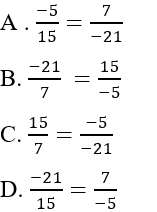

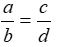 (a, b, c, d # 0) ta có thể suy ra:
(a, b, c, d # 0) ta có thể suy ra: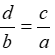 B.
B. 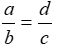
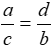 D.
D.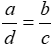
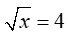 thì x bằng:
thì x bằng: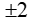 B.
B. 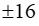 C. 2 D.16
C. 2 D.16 x-y
x-y 
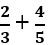 ?
?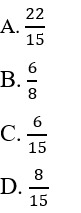
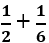 ?
?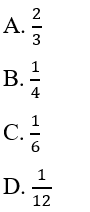
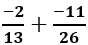
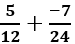
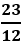 là kết quả của phép tính:
là kết quả của phép tính: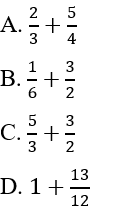
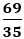 là kết quả của phép tính:
là kết quả của phép tính: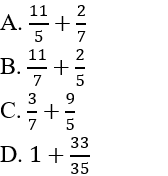
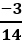 viết thành hiệu của 2 số hữu tỉ dương nào sau đây?
viết thành hiệu của 2 số hữu tỉ dương nào sau đây?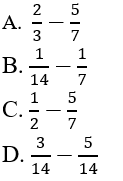
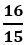 viết thành hiệu của 2 số hữu tỉ dương nào sau đây?
viết thành hiệu của 2 số hữu tỉ dương nào sau đây? nên C đúng
nên C đúng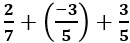
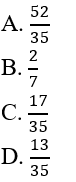 nên C đúng
nên C đúng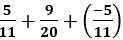
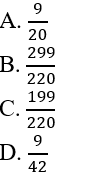 nên C đúng
nên C đúng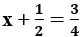 . Gía trị của x bằng:
. Gía trị của x bằng: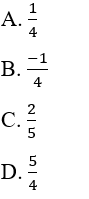 nên C đúng
nên C đúng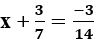 . Gía trị của x bằng:
. Gía trị của x bằng: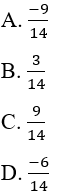 nên C đúng
nên C đúng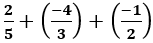 là:
là: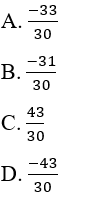
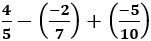 là:
là: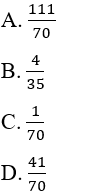
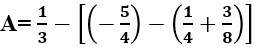
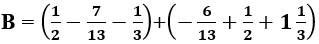
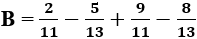
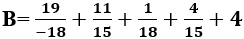
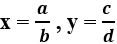 (a, b, c, d ∈ Z, b ≠ 0, d ≠ 0). Tổng x + y bằng:
(a, b, c, d ∈ Z, b ≠ 0, d ≠ 0). Tổng x + y bằng: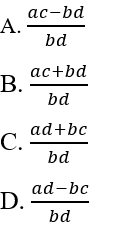
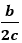 (a, b, c ∈ Z, c ≠ 0). Tổng x + y bằng:
(a, b, c ∈ Z, c ≠ 0). Tổng x + y bằng: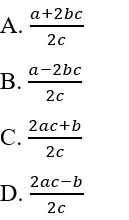
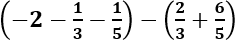 , ta được kết quả là:
, ta được kết quả là: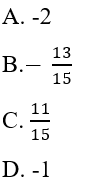
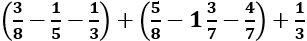 , ta được kết quả:
, ta được kết quả: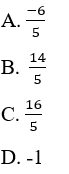
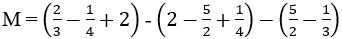
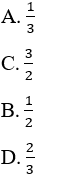
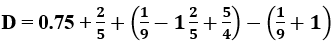

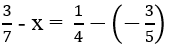
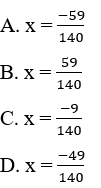
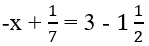
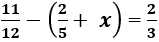
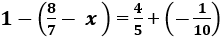

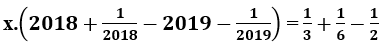
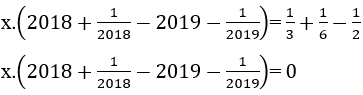
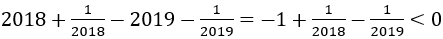 nên x = 0.
nên x = 0.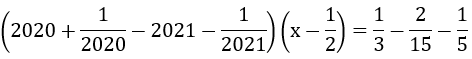
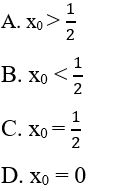
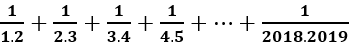 là
là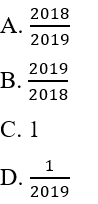
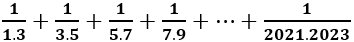 là
là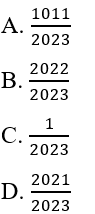
lỗi r
cm 3 dơn thức -1/2 x^3.y^4,-x^4.y^3,2xy ko thể cùng có gt âm