Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mệnh đề, tập hợp
Trong các mệnh đề sau, mệnh đề nào đúng:
- 1794 chia hết cho
- 3 π<3.15 (chọn)
- 2√ là số hữu tỉ
- Em trả lời rồi có được 3GP không học24

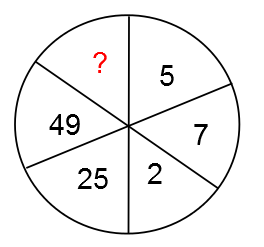
Theo đề bài ta nhận thấy số đối diện số 5 là số 25
=> Quy luật là : n2
=> 52 = 25
=> 72 = 49
<=> 22 = 4

oà, mặc dầu năm sau nữa em mới thi lớp 10 nhưng nhìn cái kiểu này...chắc chắn em sẽ "cóp". Thank you cô Ngọc!

Ta có: a:b=\(\frac{2}{7}\)=>a=\(\frac{2}{7}\)*b
Ta có:\(\frac{a+35}{b}\)=\(\frac{11}{14}\)
=>(a+35)*14=11b
=>14a+490=11b
=>14*\(\frac{2}{7}\)*b+490=11b
=>4b+490=11b
=>490=11b-4b
=>490=7b
=>b=490:7
=>b=70
=>a=70*\(\frac{2}{7}\)
=>a=20
Vậy a=20;b=70(Đề là thêm 35 đơn vị vào a;còn lại giữ nguyên)

TRẢ LỜI:
Mệnh đề phủ định của P: P− “ π không là một số hữu tỉ”.
P là mệnh đề sai, P− là mệnh đề đúng.
Mệnh đề phủ định của Q: Q− “Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh thứ ba”.
Q là mệnh đề đúng, Q− là mệnh đề sai.
tk cho mk ha

Vì Bangkok phải là Thái Lan còn thủ đô của Myanmar là Nây Pi-tô.


Đk: \(x^3+1\ge0\Leftrightarrow x\ge-1\left(1\right)\)
Đặt \(a=\sqrt{x+1};b=\sqrt{x^2-x+1}\left(a\ge0,b>0\right)\left(2\right)\Rightarrow a^2+b^2=x^2+2\)
Khi đó pt đã cho trở thành: \(10ab=3\left(a^2+b^2\right)\Leftrightarrow\left(a-3b\right)\left(3a-b\right)=0\Leftrightarrow\orbr{\begin{cases}a=3b\\b=3a\end{cases}}\)
+) Nếu a=3b thì từ (2) \(\Rightarrow\sqrt{x+1}=3\sqrt{x^2-x+1}\Leftrightarrow9x^2-10x+8=0\)( vô nghiệm)
+) Nếu b=3a thì từ (2) \(\Rightarrow3\sqrt{x+1}=\sqrt{x^2-x+1}\Leftrightarrow9x+9=x^2-x+1\Leftrightarrow x^2-10x-8=0\)
Pt có 2 nghiệm \(x_1=5+\sqrt{33};x_2=5-\sqrt{33}\left(tm\left(1\right)\right)\)





a: Có 1 giá trị x thuộc tập R thỏa mãn x^2=-10
Mệnh đề này sai vì x^2>=0>-10 với mọi x thuộc R
b: Với mọi x thực, x^2+x+12 luôn khác 0
x^2+x+12
=x^2+x+1/4+47/4
=(x+1/2)^2+47/4>=47/4>0 với mọi x
=>Mệnh đề này đúng
c: Với mọi x thuộc R thì x^2 luôn ko lớn hơn 0
Mệnh đề này sai vì ví dụ như x=1 thì 1^2>0 chứ ko bé hơn 0
d: Có một giá trị thực của x thỏa mãn x^2<=0
Mệnh đề này đúng bởi vì có x=0 thỏa mãn x^2<=0
e:
Có một giá trị x thực thỏa mãn x^2+x+5>0
Mệnh đề này đúng vì x^2+x+5=(x+1/2)^2+19/4>0 với mọi x
f: Với mọi giá trị x thực thì x^2+x+5 luôn dương
Mệnh đề này đúng