Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số héc-ta rừng đội công nhân đó trồng theo kế hoạch mỗi tuần là \(x\left(ha\right),x>0\).
Theo kế hoạch thì trồng xong trong số tuần là: \(\frac{70}{x}\)(tuần)
Theo bài ra ta có phương trình:
\(\left(\frac{70}{x}-2\right)\left(x+5\right)=75\)
\(\Rightarrow\left(70-2x\right)\left(x+5\right)=75x\)
\(\Leftrightarrow-2x^2-15x+350=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=10\left(tm\right)\\x=-17,5\left(l\right)\end{cases}}\).
Vậy theo kế hoạch mỗi tuần đội công nhân đó trồng \(10ha\)rừng.

Gọi diện tích rừng mà mỗi tuần lâm trường dự định trồng là x (ha) (Điều kiện:x >0)
Theo dự định, thời gian trồng hết 75 ha rừng là 75/x (tuần)
Vì mỗi tuần lâm trường trồng vượt mức 5ha so với dự định nên thực tế mỗi tuần lâm trường trồng được x + 5 (ha)
Do đó thời gian thực tế lâm trường trồng hết 80 ha rừng là: 80/(x+5) (tuần)
Vì thực tế lâm trường trồng xong sớm so với dự định là 1 tuần nên ta có phương trình:
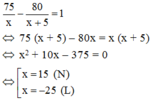
Vậy mỗi tuần lâm trường dự tính trồng 15 ha rừng
Đáp án: D

goi thoi gian moi doi phai lam theo ke hoach la x( ngay,x>0)
thoi gian doi 1 da lam la x-2 (ngay)
thoi gian doi 2 da lam la x+2 ( ngay )
moi ngay doi 1 trong duoc 40x−240x−2(ha)
moi ngay doi 2 trong duoc 90x+290x+2(ha)
neu doi 1 lam xong x+2 ngay thi trong duoc 40x−2(x+2)40x−2(x+2)(ha)
nếu đội 2 làm xong x-2 ngày thì trồng được
90x+2(x−2)(ha)90x+2(x−2)(ha)
theo de bai thi dien h rung trong duoc cua 2 doi la bang nhau nen ta co pt:
40x−2(x+2)=90(x+2)(x−2)40x−2(x+2)=90(x+2)(x−2)
=> x=10 hoac x=2/5
x2>2=> x=2/5 loai

Gọi diện tích rừng mà mỗi tuần lâm trường dự định trồng là x (ha) (Điều kiện:x >0)
Theo dự định, thời gian trồng hết 140 ha rừng là 140/x (tuần)
Vì mỗi tuần lâm trường trồng vượt mức 4 ha so với dự định nên thực tế mỗi tuần lâm trường trồng được x + 4 (ha)
Do đó thời gian thực tế lâm trường trồng hết 144 ha rừng là: 144/(x+4) (tuần)
Vì thực tế lâm trường trồng xong sớm so với dự định là 2 tuần nên ta có phương trình:
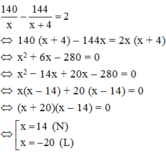
Vậy mỗi tuần lâm trường dự định trồng 14 ha rừng
Đáp án: B

Bài 1 :
Gọi số người của đội là \(x\) người \(\left(x\inℕ^∗\right)\)
Thời gian làm theo kế hoạch là \(\frac{420}{x}\) ngày
Số người lúc sau là \(x+5\) người
Thời gian hoàn thành lúc sau là \(\frac{420}{x+5}\) ngày
Vì thời gian giảm 7 ngày nên ta có phương trình :
\(\frac{420}{x}-7=\frac{420}{x+5}\)
\(\Leftrightarrow420\left(x+5\right)-7x\left(x+5\right)=420x\)
\(\Leftrightarrow420x+2100-7x^2-35x-420x\)
\(\Leftrightarrow7x^2+35x-2100=0\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow\left(x+20\right)\left(x-15\right)=0\)
\(\Leftrightarrow x=15\) \(\left(x\inℕ^∗\right)\)
Vậy số người của đội là 15 người.

a) Ta có AH là đường cao của tam giác ABC, do đó AB là đường trung trực của đoạn thẳng LH (vì H là trung điểm của BC).
b) Ta có $\angle AED = \angle ACD$ do cùng chắn cung AD trên đường tròn (T). Mà $\angle A = \angle APQ$ vì DE // PQ, nên $\angle AED = \angle APQ$. Tương tự, ta cũng có $\angle ADE = \angle AQP$. Do đó tam giác ADE và APQ đều có hai góc bằng nhau, tức là cân.
c) Ta có $\angle LBD = \angle LCB$ do cùng chắn cung LB trên đường tròn (T). Mà $\angle LCB = \angle LPB$ vì DE // PQ, nên $\angle LBD = \angle LPB$. Tương tự, ta cũng có $\angle LDC = \angle LQC$. Do đó tam giác LBD và LPQ đều có hai góc bằng nhau, tức là đồng dạng. Vậy ta có $\frac{LD}{LP} = \frac{LB}{LQ}$.
Từ đó, có $\frac{LP}{LQ} = \frac{LB}{LD}$. Áp dụng định lý cosin trong tam giác BPQ, ta có:
$PQ^2 = BP^2 + BQ^2 - 2BP \cdot BQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có:
$BP = LB \cdot \frac{LD}{LP}$
$BQ = L \cdot \frac{LP}{LD}$
Thay vào định lý cosin, ta được:
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \frac{LD}{LP} \cdot \frac{LP}{LD} \cdot \cos{\angle PBQ}$
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \cos{\angle PBQ}$
Tương tự, áp dụng định lý cosin trong tam giác ADE, ta có:
$DE^2 = AD^2 + AE^2 - 2AD \cdot AE \cdot \cos{\angle AED}$
Nhưng ta cũng có:
$AD = LD \cdot \frac{LB}{LP}$
$AE = LQ \cdot \frac{LD}{LP}$
Thay vào định lý cosin, ta được:
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \frac{LB}{LP} \cdot \frac{LD}{LP} \cdot \cos{\angle AED}$
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \cos{\angle AED}$
Nhưng ta cũng có $\angle AED = \angle PBQ$ do tam giác cân ADE và APQ, nên $\cos{\angle AED} = \cos{\angle PBQ}$. Do đó,
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LB \cdot LQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có $LB \cdot LQ = LH \cdot LL'$ (với L' là điểm đối xứng của L qua AB), do tam giác HL'B cân tại L'. Thay vào phương trình trên, ta được:
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LH \cdot LL' \cdot \cos{\angle PBQ}$

Gọi x là số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo kế hoạch
(x ∈ ℕ * , x < 84)
Số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo thực tế: x + 2
Thời gian mà công nhân hoàn thành theo kế hoạch: 84/x (h)
Thời gian mà công nhân hoàn thành theo thực tế: 84/(x+2) (h)
Người công nhân đó hoàn thành công việc sớm hơn dự định 1 giờ nên ta có phương trình:
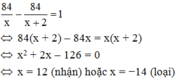
Vậy theo kế hoạch mỗi giờ người công nhân phải làm 12 sản phẩm
Đáp án: B
Đặt mỗi tuần trồng được x (ha); y là số tuần phải làm (y ≥ 1)
Ta có hệ : xy = 75 (1); (x+5) (y-1) = 80 (2)
Từ (1) ⇒ x = \(\frac{75}{y}\) thay vào 2 giải ra \(\left[{}\begin{matrix}y=5\left(tm\right)\\y=-3\left(l\right)\end{matrix}\right.\)
⇒ x = 15 (ha)