Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn trả lời:
Ta có: √2+√x=32+x=3 . Vì hai vế đều dương, ta bình phương hai vế
(√2+√x)2=32⇔2+√x=9⇔√x=7⇔(√x)2=72⇔x=49(2+x)2=32⇔2+x=9⇔x=7⇔(x)2=72⇔x=49
Chọn đáp án D

a) \(x^2=49\Rightarrow\orbr{\begin{cases}x=7\\x=-7\end{cases}}\)

\(đkxđ\Leftrightarrow\hept{\begin{cases}x\ge0\\x\ne49\end{cases}}\)
\(B=\left(\frac{\sqrt{x}}{x-49}-\frac{\sqrt{x}-7}{x+7\sqrt{x}}\right):\)\(\frac{2\sqrt{x}-7}{x+7\sqrt{x}}+\frac{\sqrt{x}}{7-\sqrt{x}}\)
\(=\left(\frac{\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+7\right)}-\frac{\left(\sqrt{x}-7\right)^2}{\sqrt{x}\left(\sqrt{x}+7\right)\left(\sqrt{x}-7\right)}\right)\)\(:\frac{2\sqrt{x}-7}{\sqrt{x}\left(\sqrt{x}+7\right)}-\frac{\sqrt{x}}{\sqrt{x}-7}\)
\(\frac{x-x+14\sqrt{x}-49}{\sqrt{x}\left(\sqrt{x}-7\right)\left(\sqrt{x}+7\right)}:\frac{2\sqrt{x}-7}{\sqrt{x}\left(\sqrt{x}+7\right)}\)\(-\frac{\sqrt{x}}{\sqrt{x}-7}\)
\(=\frac{7\left(2\sqrt{x}-7\right)\sqrt{x}\left(\sqrt{x}+7\right)}{\sqrt{x}\left(\sqrt{x}+7\right)\left(\sqrt{x}-7\right)\left(2\sqrt{x}-7\right)}\)\(-\frac{\sqrt{x}}{\sqrt{x}-7}\)
\(=\frac{7}{\sqrt{x}-7}-\frac{\sqrt{x}}{\sqrt{x}-7}=\frac{7-\sqrt{x}}{\sqrt{x}-7}=-1\)

\(a.2\sqrt{x-2}=16\left(ĐK:x\ge2\right)\Leftrightarrow\sqrt{x-2}=8\Leftrightarrow x-2=64\Leftrightarrow x=66\)
\(b.\sqrt{x-1}>3\left(ĐK:x\ge1\right)\Leftrightarrow x-1>9\Leftrightarrow x>10\)
\(c.-5\sqrt{2x+4}\le-10\left(ĐK:x\ge2\right)\\ \Leftrightarrow\sqrt{2x+4}\ge2\\ \Leftrightarrow2x+4\ge4\\ \Leftrightarrow2x\ge0\Leftrightarrow x\ge0\)
\(a.2\sqrt{x-2}=16\left(ĐK:x>2\right)\Leftrightarrow\sqrt{x-2}=8\Leftrightarrow x-2=64\Leftrightarrow x=66\)
b.\(\sqrt{x-1}>3\left(ĐK:x>1\right)\Leftrightarrow x-1>9\Leftrightarrow x>10\)
\(c.-5\sqrt{2x+4}< -10\left(ĐK:x>-2\right)\\ \Leftrightarrow\sqrt{2x+4}>2\\ \Leftrightarrow2x+4>4\\ \Leftrightarrow2x>0\Leftrightarrow x>0\)

Bài 1:
\(\left(\dfrac{x}{x^2-49}-\dfrac{x-7}{x^2+7x}\right):\dfrac{2x-7}{x^2+7x}+\dfrac{x}{7-x}\)
\(=\left(\dfrac{x}{\left(x-7\right)\left(x+7\right)}-\dfrac{x-7}{x\cdot\left(x+7\right)}\right)\cdot\dfrac{x^2+7x}{2x-7}+\dfrac{x}{-\left(x-7\right)}\)
\(=\dfrac{x^2-\left(x-7\right)^2}{x\cdot\left(x-7\right)\left(x+7\right)}\cdot\dfrac{x\cdot\left(x+7\right)}{2x-7}-\dfrac{x}{x-7}\)
\(=\dfrac{\left(x-\left(x-7\right)\right)\cdot\left(x+x-7\right)}{x-7}\cdot\dfrac{1}{2x-7}-\dfrac{x}{x-7}\)
\(=\dfrac{\left(x-x+7\right)\cdot\left(2x-7\right)}{x-7}\cdot\dfrac{1}{2x-7}-\dfrac{x}{x-7}\)
\(=\dfrac{7}{x-7}-\dfrac{x}{x-7}\)
\(=\dfrac{7-x}{x-7}\)
\(=\dfrac{-\left(x-7\right)}{x-7}\)
\(=-1\)
A = \(\left(\dfrac{x}{x^2-49}-\dfrac{x-7}{x^2+7x}\right):\dfrac{2x-7}{x^2+7x}+\dfrac{x}{7-x}\)
A = \(\left(\dfrac{x}{\left(x+7\right)\left(x-7\right)}-\dfrac{x-7}{x\left(x+7\right)}\right):\dfrac{2x-7}{x\left(x+7\right)}+\dfrac{x}{7-x}\)
A = \(\left(\dfrac{x^2-\left(x-7\right)^2}{\left(x+7\right)\left(x-7\right)x}\right):\dfrac{2x-7}{x\left(x+7\right)}-\dfrac{x}{x-7}\)
A = \(\left(\dfrac{x^2-\left(x^2-14x+49\right)}{\left(x+7\right)\left(x-7\right)x}\right):\dfrac{\left(2x-7\right)\left(x-7\right)-\left(x^3+7x^2\right)}{\left(x+7\right)\left(x-7\right)x}\)
A = \(\dfrac{14x-49}{\left(x+7\right)\left(x-7\right)x}:\dfrac{-x^3-5x^2-21x+49}{\left(x+7\right)\left(x-7\right)x}\)
A = \(\dfrac{14x-49}{\left(x+7\right)\left(x-7\right)x}.\dfrac{\left(x+7\right)\left(x-7\right)x}{-x^3-5x^2-21x+49}\)
A = \(\dfrac{14x-49}{-x^3-5x^2-21x+49}\)

1:
a: \(\sqrt{25}+\sqrt{49}=5+7=12\)
b: \(\sqrt{121}-\sqrt{81}=11-9=2\)
2: x>-2
=>2x>-4
=>2x+1>-3
=>Với x>-2 thì \(\sqrt{2x+1}\) chưa chắc có nghĩa
3:
a: \(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}\)
\(=\left|\sqrt{3}-1\right|-\sqrt{3}\)
\(=\sqrt{3}-1-\sqrt{3}=-1\)
b: \(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\cdot\sqrt{7}+7\sqrt{8}\)
\(=\left(3\sqrt{7}-2\sqrt{14}\right)\cdot\sqrt{7}+14\sqrt{2}\)
\(=21-14\sqrt{2}+14\sqrt{2}=21\)
c:
\(\dfrac{\sqrt{27}-\sqrt{108}+\sqrt{12}}{\sqrt{3}}\)
\(=\dfrac{3\sqrt{3}-6\sqrt{3}+2\sqrt{3}}{\sqrt{3}}=3+2-6=-1\)
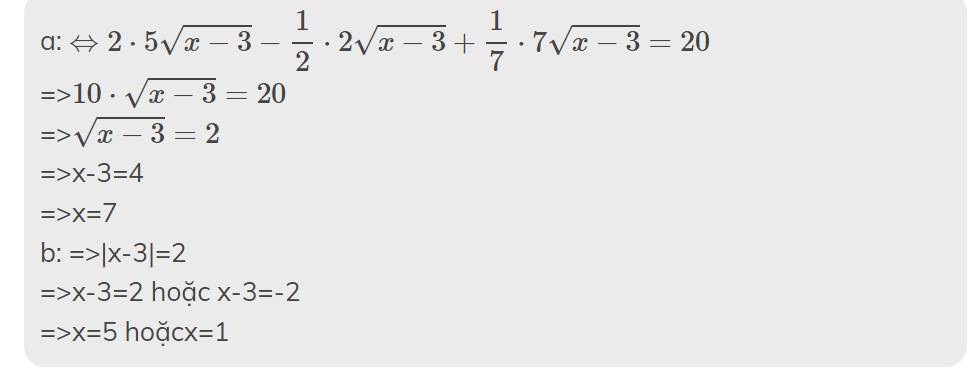
Điều kiện : x ≥ 0