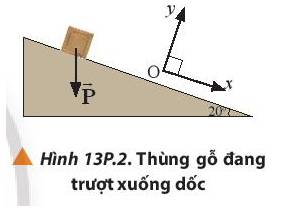
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
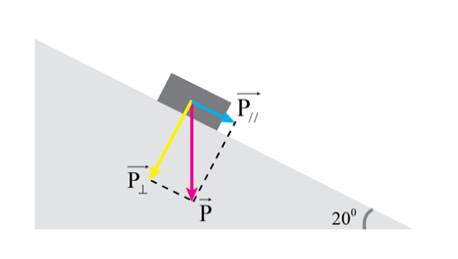
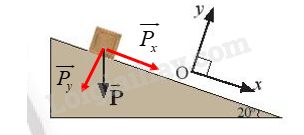
Giản đồ vectơ các lực tác dụng lên thùng hàng:

b)
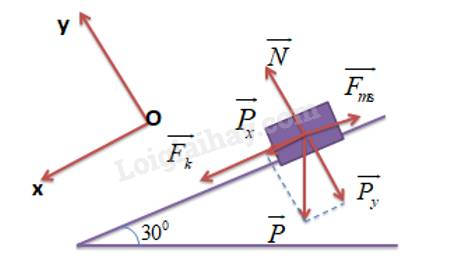
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.

a) Thế năng của thùng: W t = m g z = 700 . 10 . 3 = 21000 J
Coi thùng được nâng đều, lực phát động có độ lớn bằng trọng lực.
Độ biến thiên thế năng bằng công của trọng lực: W t - W 0 t = - A p
Công của lực phát động A F = - A p = W t = 21000 J
b) *Độ biến thiên thế năng khi hạ thùng xuống sàn ô tô:
![]()
Trong trường hợp này thế năng giảm.
*Công của trọng lực không phụ thuộc cách di chuyển hòm giữa hai vị trí vì trọng lực là lực thế, công của nó chỉ phụ thuộc vào mức độ chênh lệch giữa hai vị trí đầu và cuối mà không phụ thuộc vào dạng đường đi.

Lực ma sát tác dụng vào thùng là:
→ F m s = μ N = μ m g = 0 , 35.50.10 = 175 N
Nhận thấy Lực ma sát tác dụng vào thùng lớn hơn lực đẩy của người đẩy thùng nên thùng không chuyển động.
Đáp án: C

Công kéo vật:
\(A=F\cdot s\cdot cos\alpha=150\cdot15\cdot cos45^o=1590,99J\)
Công suất thực hiện:
\(P=\dfrac{A}{t}=F\cdot v=150\cdot1,5=225W\)

Theo định luật II Newton: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Chiếu phương trình lên Oy: \(N-P=0\Rightarrow N=P=mg=40.9,8=392\left(N\right)\)
Chiếu phương trình lên Ox: \(-F_{ms}+F=ma\)
\(\Rightarrow-\mu N+F=ma\)
\(\Rightarrow a=\dfrac{F-\mu N}{m}=\dfrac{240-0,25.392}{40}=3,55\left(\dfrac{m}{s^2}\right)\)
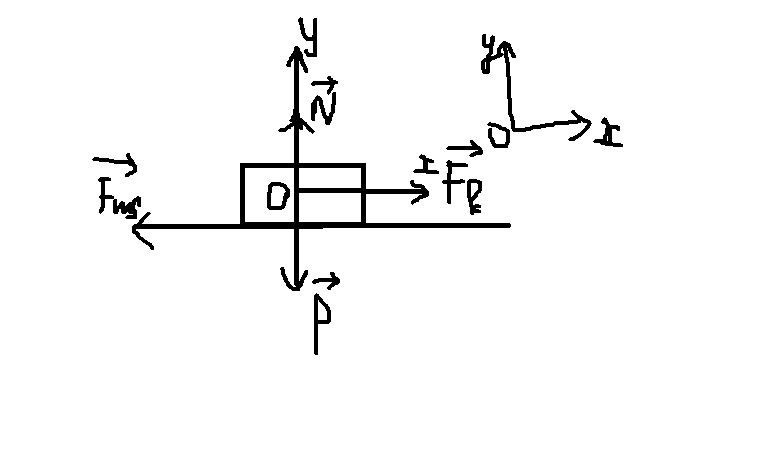
Chọn hệ trục Oxy như hình.
Chiều dương là chiều chuuyeern động.
Theo định luật ll Niu-tơn:
\(\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}=m.\overrightarrow{a}\) (1)
Chiếu lên trục Ox ta đc:
\(F-F_{ms}=ma\) (2)
Chiếu (1) lên trục Oy ta đc:
\(N-P=0\Rightarrow N=P=mg\) (3)
\(F_{ms}=\mu\cdot N\) (4)
Từ \(\left(2\right).\left(3\right),\left(4\right)\) ta suy ra:
\(F-F_{ms}=ma\)
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{240-0,25\cdot40\cdot9,8}{40}=3,55\)m/s2

Chọn chiều của lực tác dụng làm chiều dương:
F m s = μ t mg = 0,35.55.9,8 = 188,65 N ≈ 189 N
Do đó a = (F - F m s )/m = (220 - 189)/55 ≈ 0,56(m/ s 2 )

Định luật ll Niu tơn: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
\(\Rightarrow F-\mu mg=m.a\)
Gia tốc thùng:
\(\Rightarrow a=\dfrac{F-\mu mg}{m}=\dfrac{180-0,25\cdot50\cdot9,8}{50}=1,15\left(m/s^2\right)\)