Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta dùng sơ đồ hình cây để mô tả như sau:
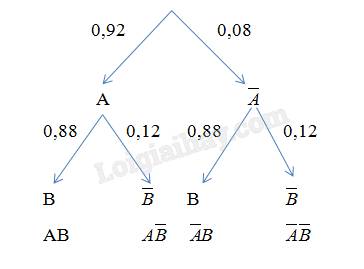
Theo sơ đồ hình cây, ta có:
a) \(P\left( {A\overline B } \right) = 0,92.0,12 = 0,1104\)
b) \(P\left( {\overline A B} \right) = 0,08.0,88 = 0,0704\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,12 = 0,0096\)
\(P\left( {A \cup B} \right) = 1 - P\left( {\overline A \overline B } \right) = 1 - 0,0096 = 0,9904\)

Lời giải:
Lấy lần 1 và lần 2 đã lấy ra được 1 sản phẩm loại I và 1 sản phẩm loại II, do đó còn $15$ sản phẩm loại I và $3$ sản phẩm loại II (tổng 18 sản phẩm)
Trong lần thứ 3:
Lấy ngẫu nhiên 1 sản phẩm, có $C^1_18=18$ cách chọn
Lấy ngẫu nhiên 1 sản phẩm loại II từ 3 sản phẩm loại II, có $C^1_3=3$ cách chọn
Xác suất để lấy được sản phẩm loại II: $\frac{3}{18}=\frac{1}{6}$