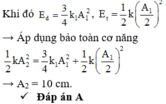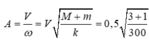Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(l_{min}=8cm\)
\(l_{max}=16cm\)
Biên độ: \(A=\dfrac{l_{max}-l_{min}}{2}=4cm\)
Cơ năng: \(W=\dfrac{1}{2}kA^2=\dfrac{1}{2}.16.(0,04)^2=0,0128J\)
Khi vật cách VTCB 2cm thì: \(\dfrac{W_t}{W}=(\dfrac{2}{4})^2=\dfrac{1}{4}\)
\(\Rightarrow W_t=\dfrac{W}{4}=\dfrac{0,0128}{4}=0,0032(J)\)

Đáp án C
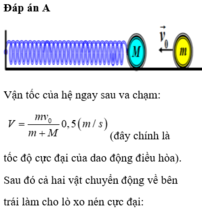
Phương pháp: Áp dụng hệ thức độc lập với thời gian của li độ và vận tốc
Cách giải:
Ta có:
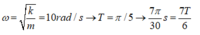
Tại thời điểm ngay trước khi giữ lò xo:
![]()
Sau khi giữ, x giảm một nửa và độ cứng tăng gấp đôi:
![]()

Chọn C
Tần số góc của dao động ω = k m = 40 0 , 4 = 10 rad/s → T = 0,2π s
+ Tại thời điểm ban đầu vật đang ở vị trí biên, sau khoảng thời gian Δ t = T + T 6 = 7 π 30 s vật đến vị trí có li độ bằng một nửa biên độ → E d = 0 , 75 E E t = 0 , 25 E
+ Giữ điểm chính giữa của lò xo, một nửa thế năng đàn hồi của lò xo sẽ mất đi theo phần chiều dài của lò xo không tham gia dao động → cơ năng của hệ dao động lúc sau sẽ là E ′ = E d + 0 , 5 E t = 0 , 875 E .
+ Với k′ = 2k, ta có 1 2 k ' A ' 2 = 0 , 875 1 2 k A 2 → A ' = A 0 , 875 2 = 8 0 , 875 2 = 2 7 c m

Hướng dẫn:
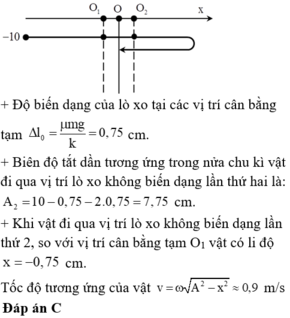
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 05.1.10 100 = 5 m m
Vật bị nén nhiều nhất khi vật chuyển động hết nửa chu kì đầu tiên
→ Trong nửa chu kì đầu vật đi được quãng đường S = 2 X 0 − x 0 = 2 10.10 − 2 − 5.10 − 3 = 0 , 19 m
→ Lực ma sát đã sinh công A = F m s S = μ m g S = 0 , 095 J .
Đáp án C