Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vị trí tương đối của hai đường tròn (O ; R) và (O’ ; r) (R ≥ r) | Hệ thức giữa OO’ với R và r | Số điểm chung | |
|---|---|---|---|
Hai đường tròn cắt nhau | R – r < OO’ < R + r | 2 | |
Hai đường tròn tiếp xúc nhau | - Tiếp xúc ngoài | OO’ = R + r | 1 |
- Tiếp xúc trong | OO’ = R – r > 0 | ||
Hai đường tròn không giao nhau | - (O) và (O’) ở ngoài nhau | OO’ > R + r | 0 |
- (O) đựng (O’) | OO’ < R - r |
Còn lại phần cuối 0 bên phải nhá Ly yêu?

1 watermelon
2 melon
3 pear
4 apple
5 grapes
6 lemon
7 orange
8 cái từ tomaao co viết sai ko nếu có thì là tomato đó xong rồi!

+ (O;R) đựng (O';r)(O′;r) có số điểm chung là 0; hệ thức giữa d,R,rd,R,r là d = R - r
+ (O;R) và (O';r)(O′;r) ở ngoài nhau có 0 điểm chung, hệ thức giữa d,R,rd,R,r là d > R + r
+ (O;R) và (O';r)(O′;r) Tiếp xúc ngoài có 1 điểm chung, hệ thức giữa d,R,rd,R,r là d = R + r
+ (O;R) và (O';r)(O′;r) Tiếp xúc trong có 1 điểm chung, hệ thức giữa d,R,rd,R,r là d = R - r
+ (O;R) và (O';r)(O′;r) cắt nhau có 2 điểm chung, hệ thức giữa d,R,rd,R,r là d < R + r
0; d<R-r
Ở ngoài nhau;0
1;d=R+r
Tiếp xúc trong;1
Cắt nhau;R-r<d<R+r

Hướng dẫn giải:
Vận dụng công thức: l = để tìm R hoặc no hoặc l. Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:
|
Bán kính R của đường tròn |
10 cm |
(40,8 cm) |
21 cm |
6,2 cm |
(21cm) |
|
Số đo no của cung tròn |
90o |
50o |
(57o) |
41o |
25o |
|
Độ dài l của cung tròn |
(15,7 cm) |
35,6 cm |
20,8 cm |
(4,4cm) |
9,2 cm |
=
Vận dụng công thức: l = để tìm R hoặc no hoặc l. Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:
|
Bán kính R của đường tròn |
10 cm |
(40,8 cm) |
21 cm |
6,2 cm |
(21cm) |
|
Số đo no của cung tròn |
90o |
50o |
(57o) |
41o |
25o |
|
Độ dài l của cung tròn |
(15,7 cm) |
35,6 cm |
20,8 cm |
(4,4cm) |
9,2 cm |

| R | d | Vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 2cm | Vì d<R nên đường thẳng cắt đường tròn. |
| 4cm | 4cm | Tiếp xúc nhau |
| 3dm | 7dm | Vì d>R nên đường thẳng và đường tròn không giao nhau. |
| R | d | vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 2cm | cắt nhau |
| 4cm | 4cm | tiếp xúc nhau |
| 3dm | 7dm | không giao nhau |

| X | -1 | -2 | 0 | 1 | 2 |
| Y=2X+3 | 2.(-1)+3=1 | 2.(-2)+3=-1 | 2.0+3=3 | 2.1+3=5 | 2.2+3=7 |

- Dòng thứ nhất: R = =
≈ 2,1 (cm)
S = π. R2 = 3,14(2,1)2 ≈ 13,8 (cm2)
Rquạt = =
≈ 1,83 (cm2)
- Dòng thứ hai: C = 2πR = 2. 3,14. 2,5 = 15,7 (cm)
S = π. R2 = 3,14(2,5)2 ≈ 19,6 (cm2)
no = =
≈ 229,3o
- Dòng thứ ba: R = =
≈ 3,5 (cm)
C = 2πR = 22 (cm)
no = =
≈ 99,2o
Điền vào các ô trống ta được các bảng sau:
|
Bán kính đường tròn (R) |
Độ dài đường tròn (C) |
Diện tích hình tròn (S) |
Số đo của cung tròn (no) |
Diện tích hình quạt tròn cung no |
|
2,1 cm |
13,2 cm |
13,8 cm2 |
(47,5o) |
1,83 cm2 |
|
(2,5 cm) |
15,7 cm |
19,6 cm2 |
229,3o |
(12,50 cm2) |
|
3,5 cm |
22 cm |
37,80 cm2 |
99,2o |
(10,60 cm2) |
Hướng dẫn giải:
- Dòng thứ nhất: R = =
≈ 2,1 (cm)
S = π. R2 = 3,14(2,1)2 ≈ 13,8 (cm2)
Rquạt = =
≈ 1,83 (cm2)
- Dòng thứ hai: C = 2πR = 2. 3,14. 2,5 = 15,7 (cm)
S = π. R2 = 3,14(2,5)2 ≈ 19,6 (cm2)
no = =
≈ 229,3o
- Dòng thứ ba: R = =
≈ 3,5 (cm)
C = 2πR = 22 (cm)
no = =
≈ 99,2o
Điền vào các ô trống ta được các bảng sau:
|
Bán kính đường tròn (R) |
Độ dài đường tròn (C) |
Diện tích hình tròn (S) |
Số đo của cung tròn (no) |
Diện tích hình quạt tròn cung no |
|
2,1 cm |
13,2 cm |
13,8 cm2 |
(47,5o) |
1,83 cm2 |
|
(2,5 cm) |
15,7 cm |
19,6 cm2 |
229,3o |
(12,50 cm2) |
|
3,5 cm |
22 cm |
37,80 cm2 |
99,2o |
(10,60 cm2) |

A C D B F E G I H O H'
a) Nối 2 điểm O và I
Vì 3 điểm H, O, I cùng nằm trên đường tròn có đường kính OH
\(\Rightarrow\) \(\Delta HIO\) nội tiếp đường tròn đường kính OH (1)
Mà OH là cạnh của \(\Delta HIO\) đồng thời cũng là đường kính (2)
Từ (1), (2) \(\Rightarrow\Delta HIO\) vuông tại I
\(\Rightarrow OI\perp HI\)
\(\Rightarrow OI\) cũng vuông góc với dây CD (3)
\(\Rightarrow IC=ID\left(4\right)\)
Ta lại có: BE \(\perp CD\left(gt\right)\left(5\right)\)
Từ (3), (5) \(\Rightarrow OI\)// BE
\(\Rightarrow OI\)// BF (6)
Mà OA = OB = R (gt) (7)
Từ (6), (7) \(\Rightarrow IA=IF\left(8\right)\)
Từ (4), (8) \(\Rightarrow ADFC\) là hình bình hành (9)
b) Từ (9) \(\Rightarrow FC=AD\left(10\right)\)
Và FC // AD
\(\Rightarrow\) \(\widehat{ICF}=\widehat{IDA}\) (2 góc so le trong) (11)
Từ (10), (11) \(\Rightarrow\Delta EFC=\Delta GAD\) (cạnh huyền - góc nhọn)
\(\Rightarrow CE=DG\) (2 cạnh tương ứng)
c) Nối 2 điểm F và H'
Ta có: HA = HO (gt) (12)
Từ (8), (12) \(\Rightarrow HI\) là đường trung bình của \(\Delta OAF\)
\(\Rightarrow HI\)// OF
\(\Rightarrow CD\)// OF (13)
Từ (5), (13) \(\Rightarrow BE\perp OF\)
\(\Rightarrow\Delta OBF\) vuông tại F (14)
Mà HO = H'O (gt) (15)
Từ (12) \(\Rightarrow HA=HO=\dfrac{1}{2}OA\left(16\right)\)
Từ (15), (16) \(\Rightarrow H'O=\dfrac{1}{2}OA\left(17\right)\)
Từ (7), (17) \(\Rightarrow H'O=\dfrac{1}{2}OB\left(18\right)\)
Mà H'O + H'B = OB
\(\Leftrightarrow\dfrac{1}{2}OB+H'B=OB\)
\(\Leftrightarrow H'B=OB-\dfrac{1}{2}OB\)
\(\Leftrightarrow H'B=\dfrac{1}{2}OB\) (19)
Từ (18), (19) \(\Rightarrow H'O=H'B\) (20)
Từ (14) \(\Rightarrow OB\) là cạnh huyền
Từ (20) \(\Rightarrow\) H' là trung điểm cạnh huyền OB của tam giác vuông OBF
\(\Rightarrow H'\)là tâm của đường tròn ngoại tiếp tam giác vuông OBF

Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
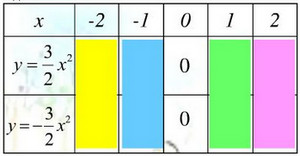
Vẽ đồ thị:
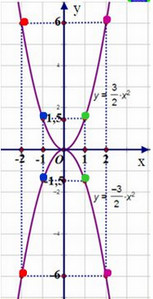
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO