Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

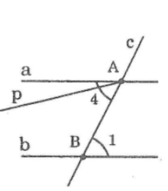
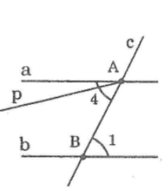
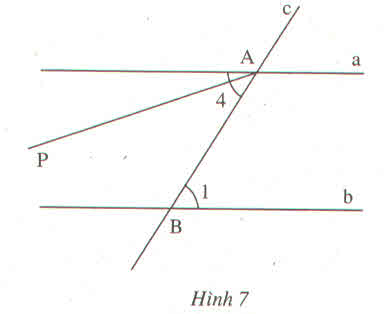
Nếu ∠(A4) ≠ ∠(B1 ) thì qua A ta vẽ tia Ap sao cho ∠(pAB) = ∠(B1)
Vì đường thẳng c cắt hai đường thẳng Ap và b và trong các góc tạo thành có cặp góc so le trong bằng nhau là: ∠(pAB) = ∠(B1). Do đó, Ap // b ( tính chất hai đường thẳng song song)
Khi đó, qua A, ta có hai đường thẳng a và Ap cùng song song với đường thẳng b (trái với tiên đề Ơ clit về đường thẳng song song).
Kết luận: đường thẳng Ap và đường thẳng a chỉ là một. Nói cách khác, ∠(pAB) = ∠(A4 ) ,từ đó ∠(A4 ) = ∠(B1)

Một cặp góc so le trong là cặp góc A4 và B1. Ta đo thấy chúng có số đo bằng nhau:
∠(A4) = ∠(B1)

* Góc đồng vị với A 1 ^ bằng 30o, khác A 1 ^ nên b1 không song song với a.
Vậy b1 không trùng với b.
* Góc kề bù với góc đồng vị của A 1 ^ bằng 145o nên góc
đồng vị với A 1 ^ bằng 180o – 145o = 35o = A 1 ^ .
Vậy b2 song song với a nên b2 trùng với b (theo tiên đề Ơ-clit)

a)
Giả thiết: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
b) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.
a) Giả thiết: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
b) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.