Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD
Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
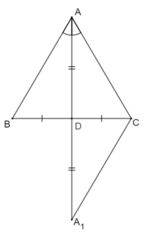
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 
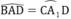(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
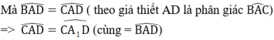
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Gọi phân số phải tìm có dạng : \(\dfrac{a}{b}\left(a⋮̸b,b\ne0\right)\)
Theo bài ra, ta có :
\(\dfrac{a+2}{2b}=\dfrac{a}{b}\\ =>\left(a+2\right)b=2ab\\ =>ab+2b=2ab\\ =>2b=ab\)
\(=>a=2\) (Do \(b\ne0\), nên chia cả 2 vế cho b)
Ta được phân số : \(\dfrac{2}{b}\left(b\ne0,2⋮̸b\right)\)
Mà phân số phải tìm lớn hơn \(\dfrac{1}{5}\) hay \(\dfrac{2}{10}\)
Do đó các phân số phải tìm là : \(\dfrac{2}{3},\dfrac{2}{4},\dfrac{2}{5},\dfrac{2}{6},\dfrac{2}{7},\dfrac{2}{8},\dfrac{2}{9}\)