Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M A N B D C E F
a, bn dựa vào hình nha
b,bn kham khảo trên h
c, Vì EFKH là hinhg bình hành nên để EFKH là hình chữ nhật thì EH⊥EF
Nối AG.
Ta lại có: EH//AG (EH là đường TB)
Và EH⊥EF EF⊥AG AG⊥BC (EF//BC)
mà ta đã có AG là đường trung tuyến của ΔABC
ΔABC cân tại A
Vâỵ để EFKH là hình chữ nhật thì tam giác ABC phải cân tại A.
Kéo dài AG cắt BC tại I
Khi đó SEFKH=EH.EF=12AG.12BC=14.23AI.BC=16AI.BC
Và SABC=BC.AI (vì ta đã CM được AI là đường cao)
SEFKHSABC=16AI.BCBC.AI=16
Vậy SEFKH=16SABC
Những gì mình làm chỉ có vậy thôi chúc bn hc tốt
A B C E F K H G
a) E là trung điểm AB, F là trung điểm AC
=> EF là đường trung bình của tam giác ABC
=> EF//BC
=> EFCB là hình bình hành
b) H là trung điểm BG, K là trung điểm CG
=> HK là đường trung bình của tam giác GBC
=> HK//=\(\frac{1}{2}\)BC
mà EF//=\(\frac{1}{2}\) BC ( vì EF là đường trung bình của tam giác ABC )
=> HK//=EF
=> HKEF là hình bình hành
c) Để EFHK là hình chữ nhật
ĐK là HE vuông EF (1)
Vì H là trung điểm BG
E là trung điểm AB
=> HE là đường trung bình BAG
=> EH//AG (2)
mà EF//BC (3)
1, 2, 3 => AG vuông BC (4)
Mặt khác G là giao điểm 2 đường trung tuyến CE, BFcủa tam giác ABC
=> G là trọng tâm
=> AG là đường trung tuyến (5)
4, 5 => Tam giác ABC cân tại A
Vậy để EFKH là hình chữ nhật thì tam giác ABC cân tại A
Gọi M là giao điểm của BC
=> Diện tích tam giác ABC :=\(\frac{1}{2}\)AM. BC
Diện tích EFKH := EF.EH=\(\frac{1}{2}\)BC.\(\frac{1}{2}\)AG=\(\frac{1}{2}\)BC. \(\frac{1}{2}\).\(\frac{2}{3}\) AM=\(\frac{1}{6}\)AM.BC =\(\frac{1}{3}\)diện tíc ABC
=> Tự so sánh nhé!

1A) Gọi I là giao điểm của EF và AB Vì EF là đường trung trực của MB nên BE=BF xét hai tam giác BEI và BFI thì chúng bằng nhau ( t. hợp ch-cgv) IE=IF; EF vuông góc AB =) E và F đối xứng nhau qua AB nên ta chứng minh được hai tam giác BEI và BF1 bằng nhau. 1b) gọi I là giao điểm của MB và EF
ta có EI là đường trung bình của tam giác MEB
nên tam giác MEB cân tại E => góc EMB = góc EBM
có EI là đường cao đồng thời là đường phân giác
nên góc MEI = góc BEI
ta có MN//BC//AD
hay ME//BF
nên góc MFI = góc IFB; góc EMB = góc FBM ( 2 góc slt)
mà góc MEI = góc BEI
nên góc IFB = góc BEI
=> tam giác BEF cân tại B
lại có BI là tia phân giác (góc EBI = góc FBI=góc EMI)
hay BI là đường trung tuyến
ta có EF vuông góc với MB
I là trung điểm của MB và EF
nên tứ giác MEBF là hình thoi 1c)*Vì EB // NC nên EBCN là hình thang có 2 đáy là EB và NC
để EBCN là hình thang cân thì EN = BC

A B C E D H K G
a) Ta có:
DE là đường trung bình của tam giác ABC =>DE//= \(\frac{1}{2}\)BC
HK là đường trung bình của tam giác GBC => HK //=\(\frac{1}{2}\)BC (1)
=> DE//=HK => DEHK là hình bình hành
b) DEHK là hình chữ nhật
điều kiện là: HE vuông góc HK
mà HE là đường trung bình tam giác ABG => HE//=\(\frac{1}{2}\)AG
lại có: HK //=\(\frac{1}{2}\)BC ( theo (1))
=> AG vuông góc BC => AG là đường cao của tam giác ABC (2)
mà hai đường trung tuyến BD và CE cắt nhau tại G => G là trọng tâm tam giác ABC => AG là đường trung tuyến ABC (3)
Từ (2), (3) => tam giác ABC cân
c) Khi BD vuông góc với CE
=> hình chữ nhật EDKH có EK vuông HD
=> EDKH là hình vuông.

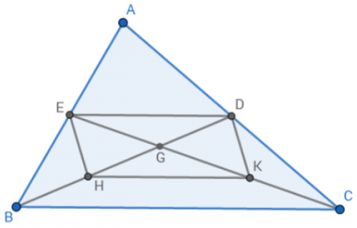
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

Sửa đề: Đường trung tuyến BD
a) Ta có: BD và CE lần lượt là các đường trung tuyến ứng với các cạnh AC,AB trong ΔABC(gt)
nên E là trung điểm của AB và D là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB(cmt)
D là trung điểm của AC(cmt)
Do đó: ED là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
H là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: HK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
Suy ra: HK//BC và \(HK=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ED//HK và ED=HKXét tứ giác EDKH có
ED//HK(cmt)
ED=HK(cmt)
Do đó: EDKH là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Sửa đề: Đường trung tuyến BD
a) Ta có: BD và CE lần lượt là các đường trung tuyến ứng với các cạnh AC,AB trong ΔABC(gt)
nên E là trung điểm của AB và D là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB(cmt)
D là trung điểm của AC(cmt)
Do đó: ED là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: ED//BC và ED=BC2ED=BC2(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
H là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: HK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
Suy ra: HK//BC và HK=BC2HK=BC2(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ED//HK và ED=HKXét tứ giác EDKH có
ED//HK(cmt)
ED=HK(cmt)
Do đó: EDKH là hình bình hành(Dấu hiệu nhận biết hình bình hành)


a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC và EF=BC/2(1)
hay EFCB là hình thang
b: Xét ΔGBC có
K là trung điểm của GB
H là trung điểm của GC
Do đó: KH là đường trung bình
=>KH//BC và KH=BC/2(2)
Từ (1) và (2) suy ra EF=HK và EF=HK
hay EFKH là hình bình hành