Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

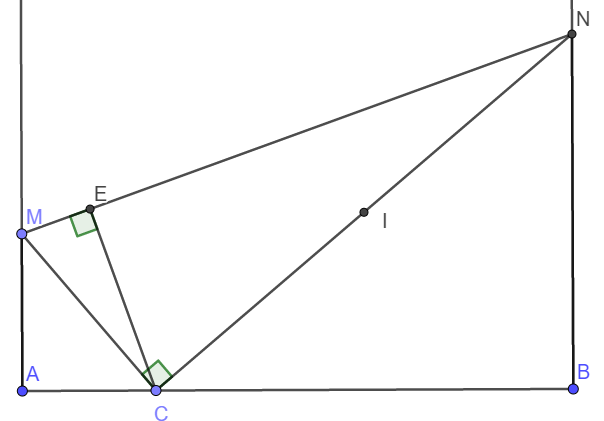
a) Tứ giác CENB có \(\widehat{CEN}=\widehat{CBN}=90^o\) nên bốn điểm B, C, E, N cùng thuộc đường tròn đường kính CN.
b) Ta có ngay \(\Delta MAC\sim\Delta CBN\left(g-g\right)\Rightarrow\frac{AM}{BC}=\frac{AC}{NB}\Rightarrow AM.BN=AC.BC\)
c) Ta có \(S_{AMNB}=\frac{\left(AM+BN\right).AB}{2}\)
Do AB, AM không đổi nên SAMNB lớn nhất khi và chỉ khi BN lớn nhất.
\(BN=\frac{AC.CB}{AM}\le\frac{\frac{\left(AC+CB\right)^2}{4}}{AM}=\frac{AB^2}{4AM}\)
Dấu bằng xảy ra khi \(AC=CB\) hay C là trung điểm AB.

câu a
Gọi H là chân đường vuông góc hạ từ M xuống tia phân giác ^BAC. Tam giác ADE có AH vừa là phân giác vùa là đường cao nên cân tại A.
Qua B vẽ BF//CE (F thuộc DE) => tam giác BDF cân tại B => BD = BF (1)
Mặt khác xét 2 tam giác BMF và CME có : BM = CM; ^BMF = ^CME ( đối đỉnh); ^MBF = ^MCE ( so le trong) => tam giác BMF = tg CME => BF = CE (2)
Từ (1) và (2) => đpcm
mấy câu còn lại bó tay