Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mot tam giac co do dai cach canh la 34dm chu vi tam giac do la

Chứng minh tam giác vuông:
Ứng dụng:
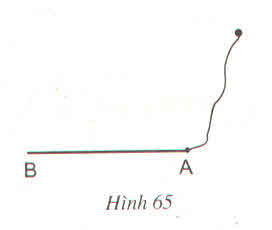
- Vẽ đường tròn (A, r) với r = AB/2; vẽ đường tròn (B, r).
- Gọi C là giao điểm của hai cung tròn nằm ở phía trong tờ giấy.
- Trên tia BC lấy D sao cho BC = CD => AB ⊥ AD.
Thật vậy: ΔABD có AC là trung tuyến ứng với BD (BC = CD) và AC = BC = CD.
=> AC = BD => ∆ABD vuông tại A.

1/ Phần này đơn giản thôi bạn! Khi chứng minh tâm của đường tròn ngoại tiếp tam giác vuồn là trung điểm cạnh huyền thì ta chứng minh ngược lại là trung điểm của cạnh huyền trong 1 tam giác vuông là tâm của đường tròn ngoại tiếp.
Giả sử ta có tam giác ABC vuông tại A và O là trung điểm của cạnh huyền BC
=> AO là đường trung tuyến ứng với cạnh huyền
=> OA = OB =OC = 1/2 BC
=> O là tâm của đường tròn ngoại tiếp tam giác ABC
Vậy ....
2/ Giả sử ta có tam giác ABC có BC là đường kính của đường tròn ngoại tiếp tam giác.
Gọi O là tâm của đường tròn ngoại tiếp tam giác ABC
=>OA = OB =OC (*)
mà BC là đường kính của đường tròn ngoại tiếp
=> O là trung điểm BC
=> OB = OC = 1/2 BC(**)
từ (*) và (**) => OA = OB = OC = 1/2 BC
=> tam giác ABC vuông tại A
@Nhoc_sieu_pham đây là toán lớp 7 mà, sao lại giải cách lớp 9 như vậy được?

toaniq.com/chung-minh-tinh-chat-duong-trung-tuyen-cua-tam-giac-vuong/
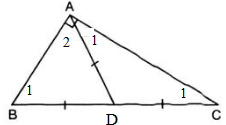
GT tam giác ABC MB = MC AM = 1/2 BC KL Tam giác ABC vuông A B C M
* Chứng minh :
ta có :
MA = MB = MC ( giả thiết )
Các tam giác MAB, MAC cân tại M
=> \(\widehat{A_1}=\widehat{B}\) ; \(\widehat{A_2}=\widehat{C}\) ( hai góc ở đáy ).
Vậy \(\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}=\widehat{A}=\widehat{B}+\widehat{C}=\frac{180^0}{2}=90^0\)
Vậy tam giác ABC vuông tại A.

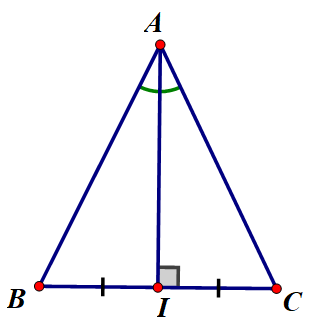
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)

A B C E D
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)

trong tam giác ABC có: đường trung tuyến AE= 1/2 BC =} tam giác ABC vuông tại A