Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABH vuông tại H và ΔADH vuông tại H có
AH chung
HB=HD
Do đó: ΔABH=ΔADH
Suy ra: AB=AD
hay ΔABD cân tại A
b: Xét ΔCBH vuông tại H và ΔCDH vuông tại H có
CH chung
BH=DH
Do đó: ΔCBH=ΔCDH
Suy ra: CB=CD
c:Xét ΔBDC có
BM là đường cao ứng với cạnh DC
CH là đường cao ứng với cạnh BD
BM cắt CH tại I
Do đó: I là trực tâm của ΔBDC
Suy ra: DI\(\perp\)BC

a) ABC cân tại A (gt) => AB=AC và góc ABC = góc ACB
=> góc ABM = góc ACN ( các góc kề bù với góc ABC và góc ACB)
Xét tam giác ABM và tam giác ACN có
AB=AC
góc ABM= góc ACN (cmt)
BM=CN )gt)
=> tam giác ABM = tam giác ACN ( c.g.c)
=> AM=AN ( 2 cạnh tương ứng)
b) tam giác ABM = tam giác ACN (cmt)
=> góc M= góc N (cặp góc tương ứng)
Xét tam giác HBM và tam giác KCN có
góc BHM= góc CKN =90 độ (BH vuông góc AM, AN vuông góc CK)
BM = CN (Gt)
góc M= góc N (cmt)
=> tam giác HBM = tam giác KCN ( cạnh huyền - góc nhọn)
c) TA có tam giác HBC và tam giác KCN (cmt)
=> góc HBM = góc KCN (hai goc tương ứng)
MÀ góc HBM = góc CBO ( hai góc đối đỉnh )
góc KCN=góc BCO ( hai góc đối đỉnh )
=> góc CBO= góc BCO
=> tam giác OBC cân tại O ( dấu hiệu nhận biết tam giác vuông)

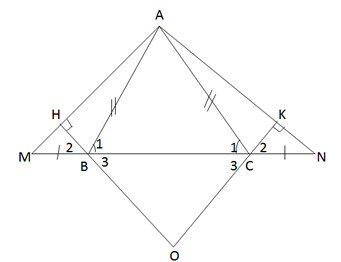
a) ∆ABC cân, suy ra ˆB1=ˆC1B1^=C1^
⇒ˆABM=ˆACN⇒ABM^=ACN^
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACNABM^=ACN^
BM = ON (gt)
Suy ra ˆM=ˆNM^=N^
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆNM^=N^ (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^
Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)
Nên ˆB3=ˆC3B3^=C3^ .
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=1800–12002=300M^=BAM^=1800–12002=300 .
Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .
Và ˆMAN=1800–(ˆAMN+ˆANM)=1800–2.300=1200MAN^=1800–(AMN^+ANM^)=1800–2.300=1200
Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.
+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)
Suy ra ˆB3=600B3^=600
Tương tự ˆC3=600C3^=600
Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).
a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có
HB=HD
AH chung
Do đó: ΔAHB=ΔAHD
Suy ra: AB=AD
Xét ΔABD có AB=AD
nên ΔABD cân tại A
b: Xét ΔCHB vuông tại H và ΔCHD vuông tại H có
CH chung
HB=HD
Do đó: ΔCHB=ΔCHD
Suy ra: CB=CD
c: Xét ΔDBC có
BM là đường cao ứng với cạnh DC
CH là đường cao ứng với cạnh BD
BM cắt CH tại I
Do đó: I là trực tâm của ΔDCB
Suy ra: DI\(\perp\)BC