Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai tam giác AHC và BAC có:
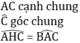
Nhưng hai tam giác này không bằng nhau vì góc AHC không phải là góc kề với cạnh AC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: \(\widehat{BAC}=70^0\)
nên \(\widehat{BAH}=35^0\)
=>\(\widehat{B}=55^0\)
=>BH<AH
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tại A

. + vì tam giác ABC là tam giác cân
=> AB=AC ( hai cạnh bên bằng nhau)
Lại có: vì góc AHC bằng 90o (gt) (1)
Mà: AHB+ AHC= 180o ( hai góc kề bù)
Từ (1) và (2) ta suy ra:
AHB= 90o và tam giác AHB là tam giác vuông
a) xét tam giác vuông ABH và tam giác ACH:
AB= AC ( cmt)
Và AHB= AHC= 90o ( cmt)
=> tam giác ABH= tam giác ACH( ch-gv)
Do đó: BH = CH ( hai cạnh tương ứng)
Vậy: H là trung điểm của BC ( đpcm)
( mình chỉ làm được câu a thoii, sorry bạn nhiều nha) 😍😘
CHÚC BẠN HỌC TỐT NHA!
a) Xét \(\Delta AHB\)và \(\Delta AHC\)có :
\(\widehat{AHB}=\widehat{AHC}\left(=90^o\right)\)
\(AB=AC\)\((\Delta ABC\)cân \()\)
AH chung
\(\Rightarrow\Delta AHB=\Delta AHC\left(ch-cgv\right)\)
\(\Rightarrow HB=HC\)( 2 cạnh tương ứng )
\(\Rightarrow\)H là trung điểm của BC
b) Xét \(\Delta MBH\)và \(\Delta NCH\)có :
\(BM=CN\left(gt\right)\)
\(\widehat{B}=\widehat{C}\)\((\Delta ABC\)cân \()\)
\(BH=HC\left(cmt\right)\)
\(\Rightarrow\Delta MBH=\Delta NCH\left(c.g.c\right)\)
\(\Rightarrow\widehat{BMH}=\widehat{CNH}\)( 2 góc tương ứng )
mà \(\widehat{BMH}=90^o\left(gt\right)\)
\(\Rightarrow\widehat{CNH}=90^o\)
\(\Rightarrow HN\perp AC\)

HB=HC
AH CẠNH CHUNG
AB=AC (CẠNH HUYỀN)
DO ĐÓ:AHB=AHC (C-C-C)
MÌNH LÀM ĐC NHIU ĐÓ CÒN NHIU BN TỰ LÀM NHÉ!!!

Qua A kẻ đường thẳng song song với BC cắt MD tại F.
Vì M là trung điểm AB nên dễ chứng minh tg AMF = tg BMD => AF = BD (1)
Mặt khác vì AD là tia phân giác ^BAH => ^BAD = ^DAH (2)
Và ^ABD = ^CAH (3) ( góc có cạnh tương ứng vuông góc)
Lấy (2) + (3) : ^BAD + ^ABD = ^DAH + ^CAH
<=> ^ADC = ^DAC => tg ACD cân tại C => AC = DC (4)
Ta có: AE/HE = AF/HD = BD/HD (5) (theo (1))
Mà BD/HD = AB/AH (6) ( tính chất phân giác)
Và AB/AH = AC/HC = DC/HC (7) ( vì tg vuông ABH ~ tg vuông CAH và theo (4))
Từ (5); (6); (7) => AE/HE = DC/HC
<=> (AH + HE)/HE = (DH + HC)/HC <=> AH/HE + 1 = DH/HC + 1 <=> AH/HE = DH/HC
=> tg vuông AHD ~ tg vuông EHC => đpcm
a, AH là tia phân giác(gt) => HAB=HAC
xét tâm giác AHB và tam giác AHC:
chung AH
HAB=HAC(cmt)
AB=AC(gt)
=>tam giác AHB bằng tam giác AHC
b, tam giác AHB bằng tam giác AHC(cmt) => AHB = AHC
có: AHB+AHC=180 (kề bù) =>AHB=AHC=90 => AH vuông góc BC
HD vuông góc AB(gt) => HDB =90 độ => tam giác HDB vuông => BHD+ABH=90 độ
AH vuông góc BC(gt) => AHB =90 độ => tam giác AHB vuông => HAB+ABH=90 độ
từ hai điều trên suy ra HAB=BHD vì cùng cộng với AHB bằng 90 độ
bạn kiểm tra hộ mik nha
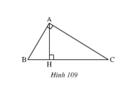


Vì AH ko bằng cạnh AB và HC ko bằng cạnh BC nên ta ko thể kết luận tam giác AHC = tam giác BAC theo trường hợp cạnh - cạnh - cạnh
Xét hai tam giác ΔAHC và ΔBAC có:
-AC chung
-Góc BAC = góc AHC
=>Ko đủ dữ kiện để kết luận hai tam giác trên bằng nhau