K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

4 tháng 3 2018
Xet ∆AED=∆CEF ( c-g-c )
=) AD=CF
Mà AD=DB
Suy ra DB=CF
b+c)
Ta có D là tđ AB
F là tđ AC
Suy ra * DE//BC
=) FDC = DCB ( slt )
* DE = 1/2BC =) BC = DF
Xét∆BDC=∆FCD ( c-g-c)
T3
3 tháng 4 2020
Cho tam giác abc có gốc a bằng 90° trên bc lấy e sao cho BE = BA tia ph . Giác của góc b cắt ac ở d
a chứng minh tam giác ABD = EBD
b tính số đo BEM
c Chứng minh BD vuông góc với AE

CM
30 tháng 7 2018
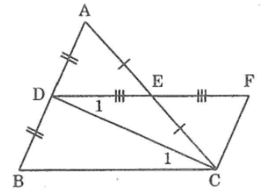
Ta có: ΔADE= ΔCFE(chứng minh trên)
⇒∠(ADE) =∠(CFE) (hai góc tương ứng)
Suy ra: AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ΔBDC và ΔFCD, ta có:
BD = CF (chứng minh trên)
∠(BDC) =∠(FCD) (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ΔBDC= ΔFCD (c.g.c)
b) Theo câu a) ta có \(\Delta ADE=\Delta CFE.\)
Hay \(BD\) // \(CF.\)
Xét 2 \(\Delta\) \(BDC\) và \(FCD\) có:
\(BD=FC\left(cmt\right)\)
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
Cạnh DC chung
=> \(\Delta BDC=\Delta FCD\left(c-g-c\right).\)
c) Theo câu b) ta có \(\Delta BDC=\Delta FCD.\)
Hay \(DE\) // \(BC.\)
+ Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> \(BC=DF\) (2 cạnh tương ứng).
+ Vì \(E\) là trung điểm của \(DF\left(gt\right)\)
=> \(DE=\frac{1}{2}DF\) (tính chất trung điểm).
Mà \(BC=DF\left(cmt\right)\)
=> \(DE=\frac{1}{2}BC\left(đpcm\right).\)
Chúc bạn học tốt!