Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N I H
Gọi khoảng cách từ A đến BM,DN lần lượt là h và k. Kẻ MH vuông góc AB.
Ta có \(S_{AMB}=\frac{MH.AB}{2}=\frac{S_{ABCD}}{2}\). Tương tự \(S_{AND}=\frac{S_{ABCD}}{2}\)
Do đó \(2S_{AMB}=2S_{AND}\) hay \(h.BM=k.DN\). Mà BM = DN nên \(h=k\)
Suy ra khoảng cách từ A đến 2 đường thẳng BM,DN là bằng nhau; BM cắt DN tại I
Vậy thì A nằm trên phân giác của ^DIB hay IA là phân giác góc DIB (đpcm).

A H B N C M D I
Gọi khoảng cách từ A đến BM,ND lần lượt là h và k. Kẻ MH vuông góc AB
Ta có : \(S_{AMB}=\frac{MH.AB}{2}=\frac{S_{ABCD}}{2}\)
Tương tự \(S_{AND}=\frac{S_{ABCD}}{2}\)
Do đó : \(2S_{AMB}=2S_{AND}\) hay \(h.BM=k.DN\)
Mà BM=DN nên h=k
Suy ra khoảng cách từ A đến hai đường thẳng BM,DN là bằng nhau; BM cắt DN tại I
Vậy thì A nằm trên phân giác của \(\widehat{DIB}\) hay IA là phân giác của góc DIB ( đpcm )

.a.
Vì `EF` là đường trung trực MB.
=> `EM=EB`
=> `ΔEMB` cân tại E
=> \(\widehat{EMB}=\widehat{EBM}\)
Chứng minh tương tự được: \(\widehat{FMB}=\widehat{FBM}\)
Vì `AM=DN` mà AM//DN
=> Tứ giác `AMND` là hình bình hành.
b.
Từ câu (a) suy ra:
ME//BF
BE//FM
=> Hình bình hành MEBF có `EF⊥MB`
=> Tứ giác MEBF là hình thoi

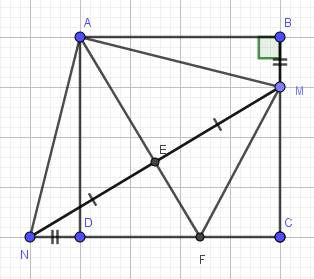
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0