

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét ∆BMI và ∆CMI, ta có:
+) BM = CM (vì IM là đường trung trực của BC)
+) \(\widehat{BMI}=\widehat{CMI}=90^0\)
+) MI cạnh chung
Suy ra: ∆BMI = ∆CMI (c.g.c)
⇒ IB = IC (hai cạnh tương ứng)
Xét hai tam giác vuông IHA và IKA, có:
+) \(\widehat{HAI}=\widehat{KAI}\) (AI là phân giác góc A)
+) AI cạnh huyền chung
Suy ra: ∆IHA = ∆IKA (cạnh huyền - góc nhọn)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông IHB và IKC, có:
+) IB = IC (chứng minh trên)
+) IH = IK (chứng minh trên)
Suy ra: ∆IHB = ∆IKC (cạnh huyền - cạnh góc vuông)
Suy ra: BH = CK (2 cạnh tương ứng)

A B C H M K I
Gọi M là trung điểm của BC
Xét hai tam giác vuông BMI và CMI có:
BM = CM (vì M là trung điểm của BC)
MI: cạnh chung
Vậy: \(\Delta BMI=\Delta CMI\left(hcgv\right)\)
Suy ra: IB = IC (hai cạnh tương ứng)
Xét hai tam giác vuông AHI và AKI có:
AI: cạnh huyền chung
\(\widehat{HAI}=\widehat{KAI}\left(gt\right)\)
Vậy: \(\Delta AHI=\Delta AKI\left(ch-gn\right)\)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông IHB và IKC có:
IB = IC (cmt)
IH = IK (cmt)
Vậy: \(\Delta IHB=\Delta IKC\left(ch-cgv\right)\)
Suy ra: BH = CK (hai cạnh tương ứng).

HÌNH TỰ VẼ NHA
Xét Δ AHI(góc H=90) và Δ AKI(góc K=90) ta có:
góc IAH = góc IAK(gt)
AI:cạnh chung
⇒ΔAHI = ΔAKI(g.c.g)
⇒IH =IK( hai cạnh tương ứng)
Xét ΔBHI (góc H=90) và ΔCKI (góc K=90) ta có:
IH =IK( hai cạnh tương ứng)
IB =IC (gt)
⇒ΔBHI = ΔCKI(ch-cgv)
⇒BH =CK( hai cạnh tương ứng)
Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
góc HAI=góc KAI
Do đó: ΔAHI=ΔAKI
=>IH=IK
Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
IH=IK
Do đó: ΔIHB=ΔIKC
=>BH=CK

Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
góc HAI=góc KAI
Do đó: ΔAHI=ΔAKI
=>IH=IK
Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
IH=IK
Do đó: ΔIHB=ΔIKC
=>BH=CK

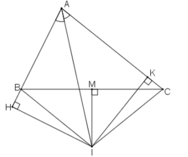
Gọi đường trung trực của BC cắt BC tại M.
Xét ΔBMI và ΔCMI, ta có:
∠(BMI) = ∠(CMI) = 90o (gt)
BM = CM ( vì M là trung điểm của BC )
MI cạnh chung
Suy ra: ΔBMI = ΔCMI(c.g.c)
Suy ra: IB = IC ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIHA và ΔIKA, ta có:
∠(HAI) = ∠(KAI) ( vì AI là tia phân giác của góc BAC).
∠(IHA) = ∠(IKA) = 90o
AI cạnh huyền chung
Suy ra: ΔIHA = ΔIKA(cạnh huyền góc nhọn)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông ΔIHB và ΔIKC, ta có:
IB = IC ( chứng minh trên )
∠(IHB) =∠(IKC) =90o
IH = IK (chứng minh trên)
Suy ra: ΔIHB = ΔIKC(cạnh huyền.cạnh góc vuông)
Suy ra: BH = CK(hai cạnh tương ứng)

1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)