VN
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DH
1
18 tháng 2 2020
Để phân số :\(\frac{2n+3}{7}\) có giá trị là số nguyên thì 2n+3:7
\(\implies\) \(2n+3=7k\)
\(\implies\) 2n=7k-3
\(\implies\) n=\(\frac{7k-3}{2}\)
Vậy với mọi số nguyên n có dang \(\frac{7k-3}{2}\) thì phân số \(\frac{2n+3}{7}\) có giá trị là số nguyên
20 tháng 6 2019
\(a,\frac{3n-2}{n+1}=\frac{3n+3-5}{n+1}=\frac{3\left(n+1\right)-5}{n+1}\)
\(=3-\frac{5}{n+1}\)
\(\text{Để }\frac{3n-2}{n+1}\in Z\)
\(\Rightarrow3-\frac{5}{n+1}\in Z\)
\(\Rightarrow n+1\inƯ\left(5\right)=\left\{1;5;-1;-5\right\}\)
\(\Rightarrow n=\left\{0;4;-2;-6\right\}\)
20 tháng 6 2019
để\(\frac{2n+1}{3n+2}\)có giá trị nguyên => \(2n+1⋮3n+2=>3\left(2n+1\right)⋮3n+2\)
\(< =>6n+3⋮3n+2\)(1)
Ta lại có : \(3n+2⋮3n+2\)với mọi n \(=>6n+4⋮3n+2\)(2)
Từ (1) và (2) suy ra \(\left(6n+4\right)-\left(6n+3\right)⋮3n+2\)<=> \(1⋮3n+2\)
Vì n là STN,do đó \(3n+2\inƯ\left(1\right)=\left(1\right)\)
Với 3n+2=1=>n=\(-\frac{1}{3}\)(loại)
Vậy k có số tự nhiên n thỏa mãn,các bài còn lại làm tương tự
20 tháng 3 2022
a, 3n−1∈Ư(12)={±1;±2;±3;±4;±6;±12}
b,
Để phân số :2n+372n+37 có giá trị là số nguyên thì 2n+3:7
\(\implies\) 2n+3=7k2n+3=7k
\(\implies\) 2n=7k-3
\(\implies\) n=7k−327k−32
Vậy với mọi số nguyên n có dang 7k−327k−32 thì phân số 2n+372n+37 có giá trị là số nguyên
:))
TN
0
PH
1
DD
Đoàn Đức Hà
Giáo viên
15 tháng 6 2021
\(\frac{2n+3}{n+2}=\frac{2n+4-1}{n+2}=2-\frac{1}{n+2}\inℤ\)
mà \(n\inℤ\Rightarrow n+2\inƯ\left(1\right)=\left\{-1;1\right\}\Leftrightarrow n\in\left\{-3;-1\right\}\).
VD
16 tháng 3 2022
\(\dfrac{2n+5}{n-3}=\dfrac{\left(2n-6\right)+11}{n-3}=\dfrac{2\left(n-3\right)+11}{n-3}=2+\dfrac{11}{n-3}\)
Để biểu thức trên là số nguyên thì \(\dfrac{11}{n-3}\) nguyên\(\Rightarrow11⋮\left(n-3\right)\)\(\Rightarrow n-3\inƯ\left(11\right)\)
Ta có bảng:
| n-3 | -11 | -1 | 1 | 11 |
| n | -8 | 2 | 4 | 14 |
Vậy \(n\in\left\{-8;2;4;14\right\}\)
16 tháng 3 2022
\(\dfrac{2n+5}{n-3}=2+\dfrac{11}{n-3}\left(n\ne3\right).\)
Để \(\dfrac{2n+5}{n-3}\in Z.\Leftrightarrow n-3\inƯ\left(11\right)\) \(=\left\{1;-1;11;-11\right\}.\)
\(\Rightarrow n\in\left\{4;2;14;-8\right\}.\)
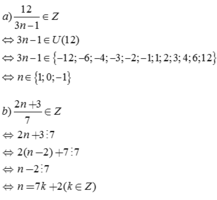
\(-\frac{3}{2n-1}\) là số nguyên \(\Leftrightarrow\)-3\(⋮\)2n-1
\(\Rightarrow2n-1\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow2n\in\left\{0;2;-2;4\right\}\)
\(\Rightarrow n\in\left\{0;1;-1;2\right\}\)
Vậy \(n\in\left\{0;1;-1;2\right\}\)
Để\(\frac{-3}{2n-1}\)có giá trị nguyên => \(-3⋮2n-1\)
=> \(2n-1\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
Ta có bảng sau :
Vậy ...