Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các góc trong một tam giác được gọi là góc trong. Các góc kề bù với góc trong được gọi là góc ngoài. Góc ngoài thì bằng tổng các góc trong không kề bù với nó. Mỗi tam giác chỉ có 3 góc trong và 6 góc ngoài.
Nhận xét: Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

Nếu : ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
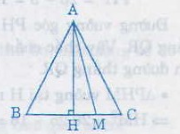
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC

Bài làm
1. hai tam giác bằng nhau là hai tam giác có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
2. tam giác ABC là tam giác đều(vẽ hình ,CM là ra)
3. trong 1 tam giác nếu bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại thì tamm giác đó là tam giác vuông.
4. tổng ba góc của 1 tam giác = 180độ , góc ngoài của tam giác = tổng 2 góc trong ko kề vs nó
5. TH1: nếu 3 cạnh của tam giác này lần lượt = 3 cạnh của tam giác kia thì 2 tam giác đó = nhau (c.c.c)
TH2 : nếu 2 cạnh và 1 óc xen giữa của tam giác này = 2 cạnh và góc xen giữa của tam giác kia thì 2 tam giác đó = nhau( c.g.c)
TH3: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau(g.c.g)
6.- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp c.g.c)
- Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g.c.g).
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (g.c.g).
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
hok tốt

1. Định nghĩa
Tam giác cân là tam giác có hai cạnh bằng nhau.
2. Tính chất.
Trong một tam giác cân hai góc ở đáy bằng nhau.
Nếu một tam giác có hai góc bằng nhau thì là tam giác cân.
Tam giác vuông cân là tam giác vuông có hai cạnh vuông góc bằng nhau.
3. Tam giác đều.(cách chứng minh)
Định nghĩa: tam giác đều là tam giác có 3 cạnh bằng nhau.
Hệ quả:
- Trong tam giác đều, mỗi góc bằng 600
- Nếu trong một tam giác có ba góc bằng nhau thì đó là tam giác đều.
- Nếu một tam giác cân có 1 góc bằng 600 thì đó là tam giác đều
Định nghĩa
Tam giác cân là tam giác có hai cạnh bằng nhau.
Tính chất.
Trong một tam giác cân, hai góc ở đáy bằng nhau.
Nếu một tam giác có hai góc bằng nhau thì là tam giác cân.
Cách chứng minh:
Chứng minh một tam giác có 2 cạnh bằng nhau thì đó là tam giác cân.
Chứng minh một tam giác có 2 góc bằng nhau thì đó là tam giác cân.
SGK toán 7