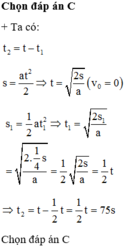Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(v\) là vận tốc ban đầu của xe.
Suy ra:
\(v_1^2-v^2=2a\dfrac{S}{4}\Rightarrow (v_1-v)(v_1+v)=2a\dfrac{S}{4}\) (1)
\(v_1=v+at_1\Rightarrow v_1-v=at_1\) (2)
Thế (2) vào (1) ta được:
\(at_1.(v_1+v)=2a\dfrac{S}{4}\Rightarrow v=\dfrac{S}{2t_1}-v_1\)
Thế vào (2) ta được: \(2v_1-\dfrac{S}{2t_1}=a.t_1\Rightarrow a = \dfrac{2v_1}{t_1}-\dfrac{S}{2t_1^2}\)
Gọi \(v_2,t_2\) là vận tốc ở cuối đoạn đường và thời gian đi hết đoạn đường đó
Suy ra
\(v_2^2-v^2=2a.S\) (3)
\(v_2=v+at_2\) (4)
Bạn thế v và a ở trên vào PT (3) và (4) rồi tính tiếp nhé.

Chọn C.
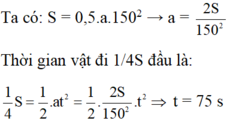
→ Thời gian vật đi 3/4 S cuối = 150 – 75 = 75 s.

Quãng đường vật chuyển động: \(S=v_0t+\dfrac{1}{2}at^2=20t+\dfrac{1}{2}at^2\)
Vật chuyển động chậm dần đều \((a=0m/s^2)\) cho đến khi vật dừng lại \((v=0m/s)\).
\(v^2-v_0^2=2aS\Rightarrow S=\dfrac{-20^2}{2\cdot a}=-\dfrac{200}{a}\left(m\right)\)
\(\Rightarrow20t+\dfrac{1}{2}at^2=-\dfrac{200}{a}\)
Mà \(v=v_0+at=20+at=0\Rightarrow a=-\dfrac{20}{t}\)
Như vậy: \(\Rightarrow20t+\dfrac{1}{2}\cdot\left(-\dfrac{20}{t}\right)\cdot t^2=-\dfrac{200}{-\dfrac{20}{t}}\)
\(\Rightarrow t=1272,7s\)
Gia tốc vật: \(a=-\dfrac{20}{1272,7}\approx-0,0157m/s^2\)