Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với: An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%).
Cách giải:
Số tiền ông A rút ra sau 5 năm đầu là: 100.1 + 8%5 ≈ 146,933 (triệu đồng)
Số tiền ông A tiếp tục gửi là: 146,933:2 ≈ 73,466 (triệu đồng)
Số tiền ông A nhận được sau 5 năm còn lại là: 73,466.1 + 8%5 ≈ 107,946 (triệu đồng)
Sau 10 năm ông A đã thu được số tiền lãi là: 107,946 - 73,466 + 146,933-100 ≈ 81,412 (triệu đồng)

Đáp án A
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với:
An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%)
Cách giải:
Số tiền ông An rút lần 1 là: 100.(1 + 8%)5 = 146,9328077 (triệu đồng)
Số tiền ông An gửi lần 2 là: 146.9328077 : 2 = 73,46640384 (triệu đồng)
Số tiền ông An rút lần 2 (gửi 5 năm tiếp theo) là:
73,46640384.(1 + 8%)5 = 107,9462499 (triệu đồng)
Số tiền lãi là: 107,9462499 - 73,4660384 = 34,47984602 ≈ 34,480 (triệu đồng).

Chọn C
Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có
P ( 1 + 0 , 068 ) 5 = 100000000
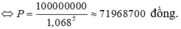
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.
Chọn C
Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có
P ( 1 + 0 , 068 ) 5 = 100000000
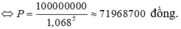
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.

Số tiền cả gốc lẫn lãi ông B nhận được sau 12 năm là:
![]()
Suy ra, số tiền lãi L ông B nhận được sau 12 năm là:
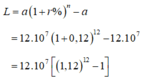
Chọn A
