Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: 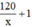 (h)
(h)
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: 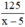 (h)
(h)
Theo bài ra ta có phương trình:
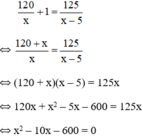
Có a = 1; b = -10; c = -600 ⇒ Δ’ = (-5)2 – 1.(-600) = 625
Phương trình có hai nghiệm phân biệt:
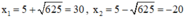
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.

Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: 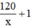 (h)
(h)
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: 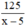 (h)
(h)
Theo bài ra ta có phương trình:
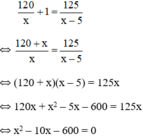
Có a = 1; b = -10; c = -600 ⇒ Δ ’ = ( - 5 ) 2 – 1 . ( - 600 ) = 625
Phương trình có hai nghiệm phân biệt:
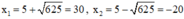
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h
Bài 43 (SGK trang 58)
Một xuồng du lịch đi từ thành phố Cà Mau đến Đất Mũi theo một đường sông dài 120 km. Trên đường đi, xuồng có nghỉ lại 1 giờ ở thị trấn Năm Căn. Khi về, xuồng đi theo đường khác dài hơn đường lúc đi 5 km và với vận tốc nhỏ hơn vận tốc lúc đi là 5 km/h. Tính vận tốc của xuồng lúc đi, biết rằng thời gian về bằng thời gian đi.
Gọi x là vận tốc lúc xuồng đi(km/h, x > 5)
thì Vận tốc lúc về sẽ là x - 5 (km/h)
Tính cả 1 giờ nghỉ ở Năm Căn thì thời gian đi từ thành phố Cà Mau đến Đất Mũi là 120x + 1 (giờ)
Quãng đường lúc về dài: 120 + 5 = 125 (km)
Thời gian đi về hết: 125x−5 (giờ)
Theo đề bài ta có phương trình:
120x + 1 = 125x−5 <=> 120(x - 5) + x(x - 5) = 125x <=> 120x - 600 + x2 - 5x - 125x = 0 <=> x2 - 10x - 600 = 0
Giải phương trình x2 - 10x - 600 = 0
Δ′ = (−5)2 - 1.(-600) = 25 + 600 = 625
√Δ′ = √625 = 25
Phương trình có hai nghiệm x1 = -(-5) + 25 = 30, x2 = -(-5) - 25 = -20
Vì x > 5 nên ta chỉ chọn giá trị x1
Vậy vận tốc xuồng lúc đi là 30 (km/h)

a) Ta có : F = av2
Khi v = 2m/s thì F = 120N nên ta có : 120 = a . 22
<=> a = 30
b) Do a = 30 nên lực F được tính bởi công thức : F = 30v2
+ Với v = 10m/s thì F(10) = 30 . 102 = 3000 ( N )
+ Với v = 20m/s thì F(20) = 30 . 202 = 12000 ( N )
c) Ta có :
90km/h = 20m/s
Với v = 25m/s thì F(25) = 30 . 252 = 18750 ( N ) > 12000 ( N )
Vậy con thuyền không thể đi được trong gió bão với vận tốc gió 90km/h
a) Quãng đường chuyển động của vật sau 1 giây là: S = 4 .12 = 4m
Khi đó vật cách mặt đất là: 100 - 4 = 96m
Quãng đường chuyển động của vật sau 2 giây là: S = 4 . 22 = 4 . 4 = 16m
Khi đó vật cách mặt đất là 100 - 16 = 84m
b) Khi vật tới mặt đất, quãng đường chuyển động của nó là 100m. Khi đó ta có:
4t2 = 100 ⇔ t2 = 25
Do đó: t = ±√25 = ±5
Vì thời gian không thể âm nên t = 5(giây)

Bài 1:
gọi CR là x, CD là x+7 (x>0,m)
theo định lý pytago: x^2+(x+7)^2=13^2
<=> x^2+x^2+14x+49=169
<=>2x^2+14x-120=0
<=>(x-5)(x+12)=0
<=>x=5(tm) hoặc x=12(loại)
vậy CR là 5m
CD là 5+7=12m