Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Chọn trục tọa độ như hình vẽ, gốc tọa độ là chỗ đặt súng, t = 0 là lúc bắn.
Phương trình quỹ đạo: 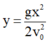
Khi hòn đá chạm đất thì y = độ cao ngọn đồi
y = g . x 2 2 v 0 2 = 100 ( m )
⇒ x = 2. y . v 0 2 g = 2.100.25 2 10 = 111,8 ( m )
Khoảng cách từ chỗ bắn đạn đến chân tường là BC = 111,8 - 100 = 11,8 m.

Đáp án B
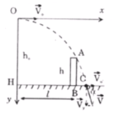
Chọn trục tọa độ như hình, gốc tọa độ là chỗ đặt súng, t = 0 là lúc bắn.
Phương trình quỹ đạo y = g x 2 2 v 0 2
Để đạn chạm đất gần chân tường nhất thì quỹ đạo của đạn sát đỉnh A của tường nên có y A = g x A 2 2 v 0 2


HD: Chọn đáp án B
Chọn trục tọa độ như hình, gốc tọa độ là chỗ đặt súng, t = 0 là lúc bắn.
Phương trình quỹ đạo:

Để đạn chạm đất gần chân tường nhất thì quỹ đạo của đạn sát đỉnh A của tường nên có:


Vị trí chạm đất là C có:

Khoảng cách từ chỗ bắn đạn đến chân tường là:
BC = 111,8 - 100 = 11,8m.

2k6 học lý 10 chuyển động ném ngang đ cần vẽ hình? :) copy ở đâu thế =))

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)

ta có: \(v_2^2=2gs_2\Rightarrow s_2=\frac{v_2^2}{2g}=\frac{30^2}{2.10}=45m\)
ta lại có:\(s=\frac{1}{2}gt^2\Leftrightarrow45=5t^2\Leftrightarrow t=3s\)
đổi 72km/h=20m/s
quãng đường tàu đi được sau 3s là:\(2gs=v_1^2\Leftrightarrow s=\frac{v_1^2}{2g}=\frac{20^2}{20}=20m\)
áp dụng định lý py-ta-go ta có:
\(45^2+20^2=s_3^2\Leftrightarrow s_3=49,24m\)
*mình k chắc đúng đâu bạn xem có sai chỗ nào không thì bảo mk nhé

Khi đến độ cao cực đại : v =0 => p=0
Bảo toàn động lượng trước và sau va chạm
\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
=> \(p_1=p_2\)
\(\Leftrightarrow\frac{m}{3}.20=\frac{2m}{3}.v_2\); \(m=\frac{m}{3}+\frac{2m}{3}\)
=> v2 = 10m/s
Ta có : \(v_2-v_2^2=2gh\)
=> \(0-10^2=2.10.h\)
=> h= 5m
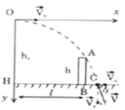



Chọn B.
Chọn trục tọa độ như hình vẽ, gốc tọa độ là chỗ đặt súng, t = 0 là lúc bắn.
Phương trình quỹ đạo
Để đạn chạm đất gần chân tường nhất thì quỹ đạo của đạn sát đỉnh A của tường nên có:
Khoảng cách từ chỗ bắn đạn đến chân tường là BC = 111,8 - 100 = 11,8 m.