Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xem Hình II.5G.
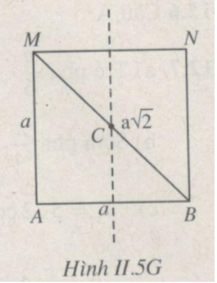
Trước hết ta tìm số vân cực đại trên toàn mặt thoáng. Đó cũng là số vân cực đại trên đoạn AB. Vì hai nguồn kết hợp dao động ngược pha nên ta có :
d 1 - d 2 = (k + 1/2) λ
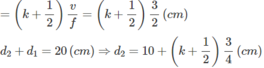
Vì 0 < d 2 < 20 (cm) ⇒ k = -13,..., -12, -1,0, 1.., 12
Bây giờ ta xét số vân cực đại trên đoạn BM.
-20 < d 2 - d 1 < 20( 2 - 1)(cm)
-20 < (k + 1/2).3/2 ≤ 2 - ( 2 - 1)
⇒ k = -13, -12 ...-1.0, 1,..., 5 ⇒ 19 điểm.
Đáp án C
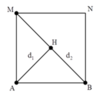
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì
d 1 - d 2 = ( k + 1 2 ) λ
+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số
+ Kết hợp hai phương trình trên ta thu được
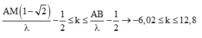
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM
Đáp án C
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì:
d 1 - d 2 = ( k + 1 2 ) λ
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.
Chọn đáp án A
Hai nguồn kết hợp ngược pha d 1 − d 2 = m λ d 1 − d 2 = k − 0 , 5 λ
Cực đại thuộc BM:
d 1 − d 2 = k + 0 , 5 λ = k + 0 , 5 1 , 5 M A − M B ≤ d 1 − d 2 < B A − B B ⇒ − 8 , 3 ≤ k + 0 , 5 1 , 5 < 20
⇒ − 6 , 03 ≤ k < 12 , 8 ⇒ k = − 6 , − 5 , − 4 , ... , 12
Vậy có 19 giá trị của k
Đáp án A
Ta có ω = 20π → f = 10Hz → λ = v/f = 3 cm.
→ AB = 40 cm = 13λ + λ/3.
Những điểm dao động với biên độ 3 2 cm cách nút những khoảng λ/4.
→ Trên AB có số điểm dao động với biên độ 3 2 cm là: 13.4 + 2 = 54 điểm.
Đáp án B
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì:
d 1 - d 2 = ( k + 1 2 ) λ
+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số d1 – d2:
AM - 2 AM ≤ d 1 - d 2 ≤ AB
+ Kết hợp hai phương trình trên ta thu được:
AM ( 1 - 2 ) λ - 1 2 ≤ k ≤ A B λ - 1 2
→ - 6 , 02 ≤ k ≤ 12 , 8
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.
$\lambda = \dfrac{3}{2}$
Vị trí cực đại thoả mãn: $(20-20\sqrt {2} \le (k+0,5)\lambda \le 20 \Rightarrow $ số $k=19$
Vậy có 19 điểm dao động biên độ cực đại trên đoạn AD.
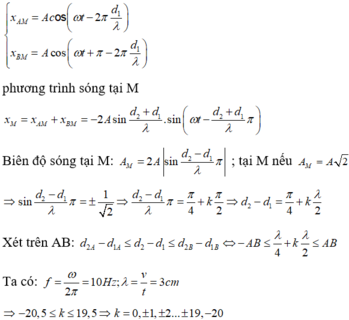
Chọn đáp án B
x A M = A c os ( ω t − 2 π d 1 λ ) x B M = A cos ( ω t + π − 2 π d 1 λ )
phương trình sóng tại M
x M = x A M + x B M = − 2 A sin d 2 + d 1 λ . sin ( ω t − d 2 + d 1 λ π )
Biên độ sóng tại M: A M = 2 A sin d 2 − d 1 λ π ; tại M nếu A M = A 2
⇒ sin d 2 − d 1 λ π = ± 1 2 ⇒ d 2 − d 1 λ π = π 4 + k π 2 ⇒ d 2 − d 1 = λ 4 + k λ 2
Xét trên AB
d 2 A − d 1 A ≤ d 2 − d 1 ≤ d 2 B − d 1 B ⇔ − A B ≤ λ 4 + k λ 2 ≤ A B
Ta có: f = ω 2 π = 10 H z ; λ = v t = 3 c m
⇒ − 20,5 ≤ k ≤ 19,5 ⇒ k = 0, ± 1, ± 2... ± 19, − 20
⇒ có 40 điểm.