Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hệ:
\(\left\{{}\begin{matrix}1,9=2\pi\sqrt{\dfrac{l}{g}}\\T_h=2\pi\sqrt{\dfrac{l}{g_h}}\end{matrix}\right.\)
Xét tỉ lệ:
\(\Rightarrow\dfrac{T_h}{1,9}=\sqrt{\dfrac{G\cdot\dfrac{M}{R^2}}{G\cdot\dfrac{M'}{\left(R+h\right)^2}}}=\sqrt{\dfrac{\dfrac{81M'}{\left(3,7R'\right)^2}}{\dfrac{M'}{R'^2}}}\)
\(\Rightarrow T_h=4,62s\)

\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

\(\overrightarrow {g'} =\overrightarrow g - \overrightarrow a \)
Ô tô chuyển động nằm ngang => \(\overrightarrow a \bot \overrightarrow g\)
=> \(g' = \sqrt{g^2+ a^2}\)
\(T = 2\pi \sqrt{\frac{l}{g}}\)
\(T' = 2\pi \sqrt{\frac{l}{g'}}\)
=> \(\frac{T}{T'} = \sqrt{\frac{g'}{g}} = \sqrt{\frac{\sqrt{g^2+a^2}}{g}} = 1,01\)
=> \(T'= \frac{2}{1,01} = 1,98 s.\)
cho mình hỏi: Nếu trong trường hợp ôtô chuyển động thẳng chậm dần đều thì phải làm ntn ?

Chu kỳ dao động nhỏ của con lắc là
\(T=2\pi\sqrt{\frac{l}{9}}\Rightarrow T=2\pi\sqrt{\frac{0,36}{\pi^2}}=1,2\left(s\right)\)
Chọn A
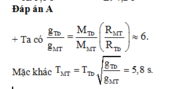
Đáp án D