Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
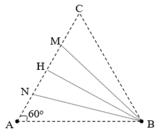
+ Khoảng cách giữa hai cực đại liên tiếp trên AB là 0,5l
+ Vì trên AB có 14 cực đại nên: 7 λ < A B = a ≤ 8 λ
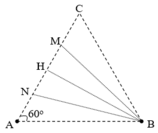
+ Gọi N và M là hai điểm cực đại cùng pha liên tiếp trên AC
Điều kiện cực đại liên tiếp:
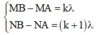
Þ NB – MB + MA – NA = l Û NB – MB + MN = l (1)
Điều kiện cùng pha liên tiếp:
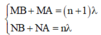
Þ MB – NB + MA – NA = l Û MB – NB + MN = l (2)
Từ (1) và (2) suy ra NB = MB Þ MN = l
+ Gọi H là trung điểm của NM Þ BH ^ AH Þ BH là đường cao trong tam giác đều hạ từ B đến AC. Ta có:
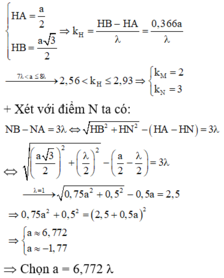

Đáp án B
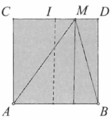
Theo đề, trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại nên:
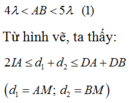
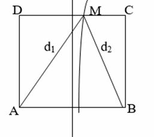
Vì I là trung điểm CD, ABCD là hình vuông nên
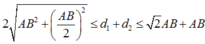
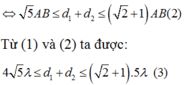
Vì hai nguồn A, B đồng pha nên giả sử:
![]()
Lúc đó, phương trình dao động tại điểm M là:
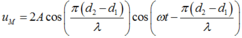
M là cực đại giao thoa bậc nhất:
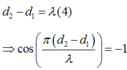
Để M dao động ngược pha với các nguồn thì:
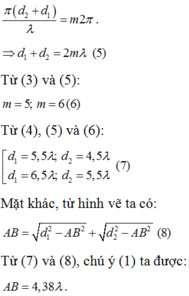

Chọn đáp án D.
Không mất tính tổng quát giả sử λ = 1.
Ta có:
Vì trên AB có 11 vị trí cực đại nên suy ra 5 < λ < 6.
(Dựa vào các đáp án suy ra chỉ có 5,3λ thỏa mãn).
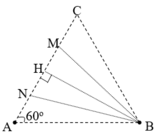



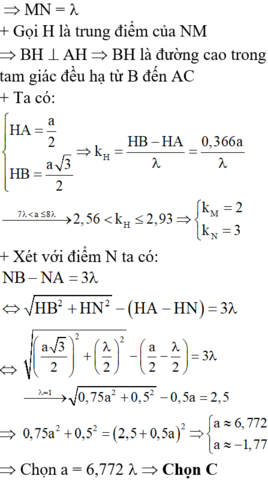
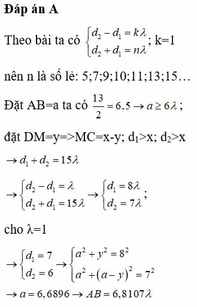


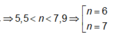
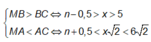
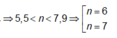
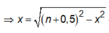
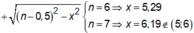


Chọn D
+ Xét N và M là hai điểm cực đại cùng pha liên tiếp trên AC
Điều kiện cực đại liên tiếp:
NB – MB + MA – NA = λ ⇔ NB – MB + MN = λ (1)
Điều kiện cùng pha liên tiếp:
⇒ MB – NB + MA – NA = λ => MB – NB + MN = λ (2)
Cộng vế với vế của (1) và (2) ta được 2MN =2 λ =>NB=MB =>tam giác NBM cân; H là trung điểm của NM => BH ⊥ AH=>BH là đường cao trong tam giác đều ABC. Ta có:
Xét điểm N: