Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

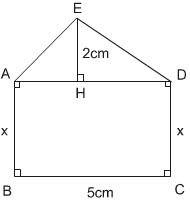
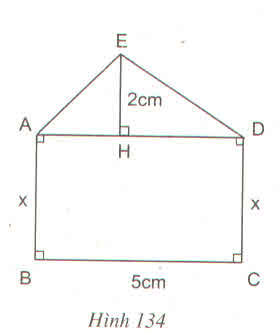
Ta có AD = BC = 5cm
Diện tích ∆ADE: SADE =  2.5 = 5(cm)
2.5 = 5(cm)
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có
SABCD= 3SADE nên 5x = 3.5
Vậy x = 3cm

Trong mỗi hình trên ta đều có:
Diện tích hình chữ nhật là: a.h
Diện tích tam giác là: 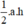
⇒ Diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.

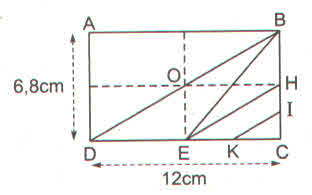
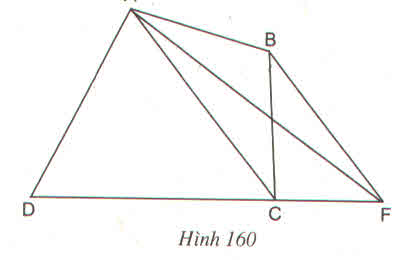
a)Ta có: DE=12DC(=12.12=6(cm)DE=12DC(=12.12=6(cm)
Nên SDBE=12.DE.BC=12.6.6,8=20,4(cm3)SDBE=12.DE.BC=12.6.6,8=20,4(cm3)
b)Ta có : HC=12BC=12.6,8=3,4(cm)HC=12BC=12.6,8=3,4(cm)
HI=12HC=12.3,4=1,7(cm)HI=12HC=12.3,4=1,7(cm)
EC = DE = 6cm
EK=KC=12EC=12.6=3(cm)EK=KC=12EC=12.6=3(cm)
Do đó SEHIK=SEHK+SHKI=12EK.HC+12HI.KCSEHIK=SEHK+SHKI=12EK.HC+12HI.KC
= 12EK.HC+12EK.HI=12EK(HC+HI)12EK.HC+12EK.HI=12EK(HC+HI)
SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)
Cách khác:
SEHIK=SEHC−SKIC=12EC.HC−12KC.ICSEHIK=SEHC−SKIC=12EC.HC−12KC.IC
= 12.6.3,4−12.3.1,712.6.3,4−12.3.1,7
= 10,2−2,55=7,65(cm2)

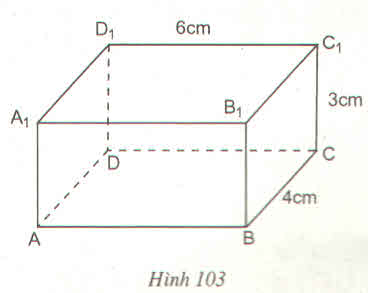
\(S_{XQ}=\left(4+6\right)\cdot2\cdot3=60\left(cm^2\right)\)
\(S_{TP}=60+24\cdot2=108\left(cm^2\right)\)

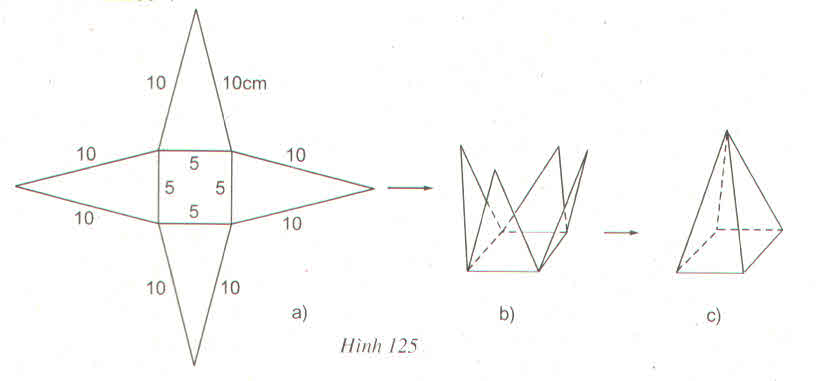
a) Trong hình 125a có 4 tam giác cân bằng nhau.
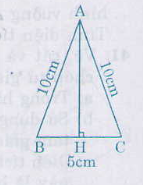
b) Chiều cao ứng với đáy của mỗi tam giác:
\(AH=\sqrt{AC^2-HC^2}\)
\(=\sqrt{AC^2-\left(\dfrac{1}{2}.5\right)^2}=\sqrt{100-\dfrac{25}{4}}=9,68\left(cm\right)\)
c) Diện tích xung quanh hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).5.4.9,68 = 96,8 (cm2 )
Diện tích đáy:
Sđ = 52 = 25 (cm2 )
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 121,8 (cm2 )
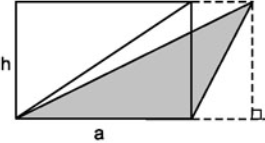
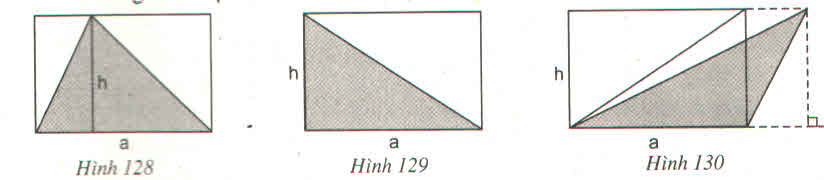
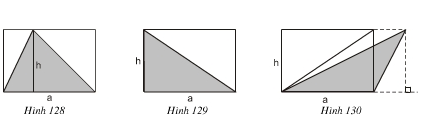



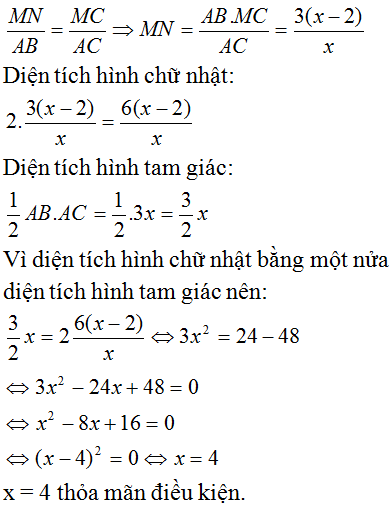

Ở hình trên, diện tích hình chữ nhật bằng....hai......... lần diện tích của tam giác được tô đậm.