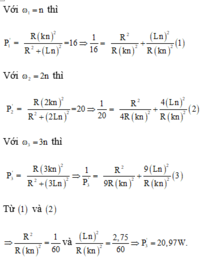Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.
Điện áp từ máy phát cấp cho mạch là: ![]() (giả sử chọn điều kiện ban đầu sao cho
(giả sử chọn điều kiện ban đầu sao cho ![]() ) ; với
) ; với
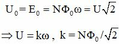
Công suất tiêu thụ là
P= 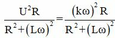
= 20,7W

Giải thích: Đáp án C
*Công suất tiêu thụ của đoạn mạch RL khi nối vào máy phát điện xoay chiều một pha.

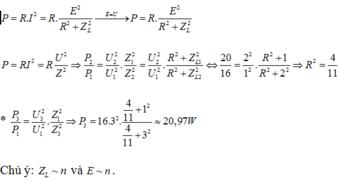

Đáp án A
Ta có: E = ωΦ = 2πfΦ = 2π.np.Φ => E tỉ lệ thuận với n.
ZL = ωL = 2πf.L = 2π.np.L => E tỉ lệ thuận với n.
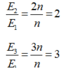
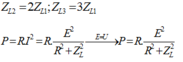
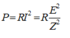
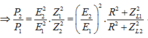
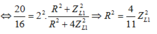
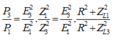
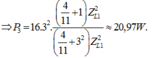

Đáp án: D
Điện áp từ máy phát cấp cho mạch là: u = U 0 cos ω t (giả sử chọn điều kiện ban đầu sao cho φ = 0 ); với U 0 = E 0 = N Φ 0 ω = U 2
⇒ U = k ω ; với k = N Φ 0 2
Công suất tiêu thụ là
P = R I 2 = U 2 R R 2 + L ω 2 = k ω 2 R R 2 + L ω 2
Với ω 1 = n thì
P 1 = R k n 2 R 2 + L n 2 = 16 ⇒ 1 16 = R 2 R k n 2 + L n 2 R k n 2 ( 1 )
Với ω = 2 n thì
P 2 = R 2 k n 2 R 2 + 2 L n 2 = 20 ⇒ 1 20 = R 2 4 R k n 2 + 4 L n 2 R k n 2 ( 2 )
Với ω 3 = 3 n thì
P 3 = R 3 k n 2 R 2 + 3 L n 2 ⇒ 1 P 3 = R 2 9 R k n 2 + 9 L n 2 R k n 2 ( 3 )
Từ (1) và (2)
⇒ R 2 R k n 2 = 1 60 và
L n 2 R k n 2 = 2 , 75 60 ⇒ P 3 = 20 , 97 W.

Đáp án C
Chú ý E tỉ lệ thuận với n. Chuẩn hóa R = 1. Áp dụng công thức tính ![]()

Chọn đáp án B
I ' I = k R 2 + Z L 2 R 2 + k Z L 2 ⇒ 3 1 = 3 · R 2 + Z L 2 R 2 + 3 Z L 2 ⇒ Z L = R 3

U=E=2πnNBS/60\(\sqrt{2}\)
I=\(\frac{U}{Z}\)=\(\frac{E}{\sqrt{R^2+Z^2_L}}\)

Chuẩn hóa R = 1
Gọi x là cảm kháng của cuộn dây khi roto quay với tốc độ n vòng/phút
Ta có I 1 I 2 = U 1 Z 2 U 2 Z 1 = 1 2 + 3 x 2 3 1 2 + x 2 = 1 3 ⇒ x = 1 3
→ Vậy khi roto quay với tốc độ 2n vòng/phút thì cảm kháng của đoạn mạch là
Đáp án B

Ta có:
\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R\)
\(4P=\dfrac{U_{2}^{2}}{Z_{2}^{2}}R\)
\(\Rightarrow \dfrac{P}{4P}=\left( \dfrac{U_{1}}{U_{2}} \right)^{2}\left( \dfrac{Z_{2}}{Z_{1}} \right)^{2}\)
\(\Leftrightarrow \dfrac{1}{4}=\left(\dfrac{n_{1}}{n_{2}} \right)^{2}\left(\dfrac{Z_{2}}{Z_{1}} \right)^{2}\rightarrow Z_{2}=Z_{1}\)
Ta nghĩ đến bài toán f biến thiên có 2 giá trị của f mạch cho cùng 1 tổng trở.\(\Rightarrow n_{0}=\sqrt{n_{1}n_{2}}=\sqrt{2}n \)
Vậy khi roto quay với tốc độ \(\sqrt{2}n\) mạch xảy ra cộng hưởng.
Công suất: \(P_0=\dfrac{U_{0}^{2}}{R}\)
Lại có:
\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R=\dfrac{U_{1}^{2}}{2R^{2}}R=\dfrac{U_{1}^{2}}{2R}\) (Do \(Z_1=\sqrt 2.R\))
\(\Rightarrow \dfrac{P}{P_{0}}=\dfrac{U_{1}^{2}}{2U_{0}^{2}}=\dfrac{1}{2}\left(\dfrac{n_{1}}{n_{0}} \right)^{2}=\dfrac{1}{4} \Rightarrow P_{0}=4P\)
Vậy: \(P_0=4P\)
\(U_0=\omega\phi\)
\(P=I^2R=\left(\frac{U_0}{Z\sqrt{2}}\right)^2R=\frac{\omega^2\phi^2R}{2\left(R^2\left(\omega L-\frac{1}{\omega c}\right)^2\right)}\)
\(=\frac{\phi^2R}{2\left(\frac{R^2}{\omega^2}+\left(L-\frac{1}{\omega^2c}\right)^2\right)}=\frac{\phi^2R}{2\left(\frac{1}{\omega^4C^2}+\frac{R^2-2L}{\omega^2}+L^2\right)}\)
Do đó: \(\phi\) không đổi. Đặt : \(\frac{1}{\omega^2}=x\)
Xét f (x) \(=\frac{x^2}{C^2}+\left(R^2-2L\right)x+2L^2\)
=> P_max \(\Leftrightarrow x_0=\frac{2L-R^2}{2C^2}\)
Do P phụ thuộc hàm bậc 2 nên
\(P_1=P_2\Rightarrow x_1+x_2=2x_0\Leftrightarrow\frac{1}{\omega^2_1}+\frac{1}{\omega^2_2}=\frac{2}{\omega^2_0}\)
Mặt khác, tốc độ quay của rôto tỉ lệ thuận với tần số góc nên
\(\frac{1}{n^2_1}+\frac{1}{n^2_2}+\frac{1}{n^2_0}\Leftrightarrow n_0=2\frac{n^2_1n^2_2}{n^2_1+n^2_2}\)