K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 8
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64=8^2\)
=>AC=8(cm)
Xét ΔABC vuông tại A có \(\sin C=\frac{AB}{BC}=\frac{6}{10}=\frac35\)
nên \(\hat{C}\) ≃37 độ
ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
=>\(\hat{B}=90^0-37^0=53^0\)
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\) (2)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
\(AE\cdot AB=AH^2\)
=>\(AE=\frac{AH^2}{AB}\)
\(AF\cdot AC=AH^2\)
=>\(AF=\frac{AH^2}{AC}\)
Xét tứ giác AEHF có \(\hat{AEH}=\hat{AFH}=\hat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>\(S_{AEHF}=AE\cdot AF=\frac{AH^2}{AB}\cdot\frac{AH^2}{AC}=\frac{AH^4}{AH\cdot BC}=\frac{AH^3}{BC}\)
18 tháng 8
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64=8^2\)
=>AC=8(cm)
Xét ΔABC vuông tại A có \(\sin C=\frac{AB}{BC}=\frac{6}{10}=\frac35\)
nên \(\hat{C}\) ≃37 độ
ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
=>\(\hat{B}=90^0-37^0=53^0\)
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\) (2)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
\(AE\cdot AB=AH^2\)
=>\(AE=\frac{AH^2}{AB}\)
\(AF\cdot AC=AH^2\)
=>\(AF=\frac{AH^2}{AC}\)
Xét tứ giác AEHF có \(\hat{AEH}=\hat{AFH}=\hat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>\(S_{AEHF}=AE\cdot AF=\frac{AH^2}{AB}\cdot\frac{AH^2}{AC}=\frac{AH^4}{AH\cdot BC}=\frac{AH^3}{BC}\)
15 tháng 8
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100=10^2\)
=>BC=10(cm)
Xét ΔABC vuông tại A có \(\sin C=\frac{AB}{BC}=\frac{6}{10}=\frac35\)
nên \(\hat{C}\) ≃37 độ
ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
=>\(\hat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔABD vuông tại A có AK là đường cao
nên \(BK\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BK\cdot BD\)
c: \(BH\cdot BC=BD\cdot BK\)
=>\(\frac{BH}{BK}=\frac{BD}{BC}\)
=>\(\frac{BH}{BD}=\frac{BK}{BC}\)
Xét ΔBHK và ΔBDC có
\(\frac{BH}{BD}=\frac{BK}{BC}\)
góc HBK chung
Do đó: ΔBHK~ΔBDC
=>\(\hat{BKH}=\hat{BCD}=\hat{ACB}\)
22 tháng 8
a: ta có: AH⊥CD
OM⊥CD
BK⊥CD
Do đó: AH//OM//BK
Xét ΔAKB có
O là trung điểm của AB
ON//KB
DO đó: N là trung điểm của AK
=>AN=NK
b: Xét hình thang ABKH có
O là trung điểm của AB
OM//AH//BK
Do đó: M là trung điểm của HK
=>MH=MK
c: ΔOCD cân tại O
mà OM là đường cao
nên M là trung điểm của CD
Ta có: MC+CH=MH
MD+DK=MK
mà MC=MD và MH=MK
nên CH=DK
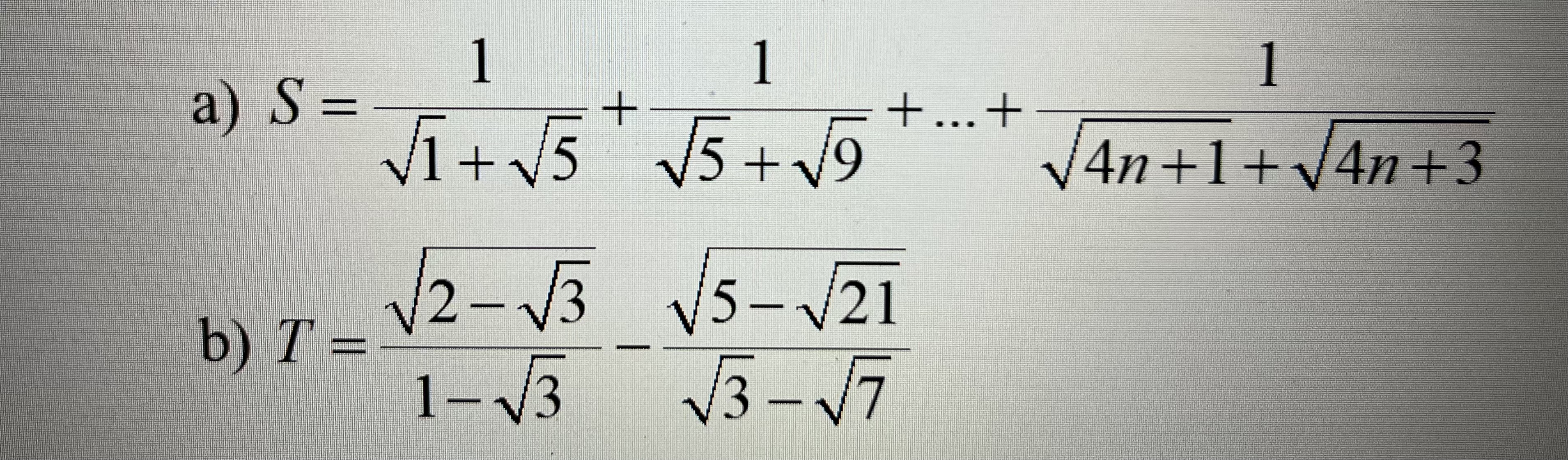
a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)