
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


xét tam giác cân ABH
=>AB2=BH2+AH2
=>92=32+AH2
=>81=9+AH2
=>AH2=81-9
=>AH2=72
=>AH=6\(\sqrt{2}\)
xé tam giác vuông AHC
=>AC2=AH2+HC2
=>112=(6\(\sqrt{2}\))2+HC2
=>HC2=121-(6\(\sqrt{2}\))2
=>HC2=49
=>HC=\(\sqrt{49}\)=7(Đ/A cần tính)

\(\left|2x+3\right|+2x=-4\)
\(\Leftrightarrow\left|2x+3\right|=-4-2x\)(1)
*Nếu \(x\ge\frac{-3}{2}\)thì \(2x+3\ge0\Rightarrow\left|2x+3\right|=2x+3\)
\(\Rightarrow\left(1\right)\Leftrightarrow2x+3=-4-2x\Leftrightarrow4x=-7\Leftrightarrow x=\frac{-7}{4}\left(L\right)\)
*Nếu \(x< \frac{-3}{2}\)thì \(2x+3< 0\Rightarrow\left|2x+3\right|=-2x-3\)
\(\Rightarrow\left(1\right)\Leftrightarrow-2x-3=-4-2x\Leftrightarrow0=-1\left(L\right)\)
Vậy pt vô nghiệm
\(\left|2x+3\right|+2x=-4\)
\(\Leftrightarrow\left|2x+3\right|=-4-2x\)
\(\Leftrightarrow\orbr{\begin{cases}2x+3=-4-2x\\2x+3=-\left(-4-2x\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x+2x=-4-3\\2x+3=4+2x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}4x=-7\\2x-2x=4-3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{7}{4}\\0=1\left(loại\right)\end{cases}}\)
Vậy : \(x=-\frac{7}{4}\)

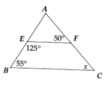
Xét tam giác ABC có:
\(\widehat{BEF}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này là 2 góc kề bù
=> EF//BC
=> \(\widehat{AFE}=\widehat{ACB}\)(2 góc đồng vị)
\(\Rightarrow x=50^0\)

giả thiết: 1 đường thẳng vuông góc với một trong 2 đường thẳng
kết luận: nó vuông góc với đường thẳng còn lại.
BẬT MÍ CHO BẠN NÈ: GIẢ THIẾT LÀ NHỮNG CHỮ Ở SAU TỪ ''NẾU''
KẾT LUẬN LÀ NHỮNG CHỮ SAU TỪ THÌ
a b c

a: 26⋅33=(22⋅3)3=12326⋅33=(22⋅3)3=123
b: 64⋅83=24⋅34⋅29=213⋅3464⋅83=24⋅34⋅29=213⋅34
c: 16⋅81=36216⋅81=362
d: 254⋅28=1004

Qua B vẽ đường thẳng Bz song song với Ax
Bz // Ax suy ra góc BAx = ABz =30 ( hai góc so le trong)
Bz // Cy suy ra góc BCy = CBz =40
suy ra ABC = ABz + CBz = 30+40 =70 độ


a: Xét ΔAHI và ΔADI có
AH=AD
HI=DI
AI chung
Do đó: ΔAHI=ΔADI
b: Ta có: ΔADH cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
c: Xét ΔHAK và ΔDAK có
AH=AD
\(\widehat{HAK}=\widehat{DAK}\)
AK chung
Do đó: ΔHAK=ΔDAK
Suy ra: \(\widehat{ADK}=\widehat{AHK}=90^0\)
=>DK⊥AC
mà AC⊥AB
nên KD//AB

a) Xét tg ABE và KBE có :
BD-chung
\(\widehat{ABD}=\widehat{KBD}\left(gt\right)\)
\(\widehat{AEB}=\widehat{KEB}=90^o\)
=> Tg ABE=KBE(g.c.g)
=> AB=BK
=> Tg ABK cân tại B
b) Xét tg ABD và KBD có :
AB=BK(cmt)
BD-chung
\(\widehat{ABD}=\widehat{DBK}\left(gt\right)\)
=> Tg ABD=KBD (c.g.c)
\(\Rightarrow\widehat{BAD}=\widehat{BKD}=90^o\)
\(\Rightarrow DK\perp BC\)
c) Do tg BAD=BKD (cmt) => AD=DK
=> Tg ADK cân tại D
\(\Rightarrow\widehat{KAD}=\widehat{AKD}\)
Mà \(\widehat{AKD}=\widehat{KAH}\)(AH//DK do cùng vuông BC)
\(\Rightarrow\widehat{KAH}=\widehat{KAD}\)
=> AK là tia pg góc HAC
d) Xét tg ABI và KBI có :
BI-chung
AB=BK (cmt)
\(\widehat{ABI}=\widehat{KBI}\left(gt\right)\)
=> Tg ABI=KBI (c.g.c)
=> AI=IK
=> Tg AIK cân I
\(\Rightarrow\widehat{IAK}=\widehat{IKA}\)
Mà : \(\widehat{IAK}=\widehat{KAD}\left(cmt\right)\)
\(\Rightarrow\widehat{IKA}=\widehat{KAD}\)
Mà chúng là 2 góc SLT => IK//AD
#H