Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(x^3+y^3=9< =>\left(x+y\right)\left(x^2-xy+y^2\right)=9\)
\(< =>x^2-xy+y^2=3\)
\(< =>\left(x+y\right)^2-3xy=3\)
\(< =>3xy=6< =>xy=2\)
giờ bạn chỉ cần giải hpt đơn giản này là đc nhé
Ta có : pt 1 <=> xy(x+y) = 2
kết hợp với pt 2 ta được \(x^2y^2+xy+1=3xy\)
\(< =>\left(xy+2\right)^2-\sqrt{3}^2=0\)
\(< =>\left(xy+2-\sqrt{3}\right)\left(xy+2+\sqrt{3}\right)=0\)
\(< =>\orbr{\begin{cases}xy=2-\sqrt{3}\\xy=2+\sqrt{3}\end{cases}}\)
đến đây dễ r , sai chỗ nào bạn chỉ mình nhé

6. \(\hept{\begin{cases}x^2-3x=y\\y^2-3y=x\end{cases}}\)
\(\Rightarrow x^2-3y-y^2+3x=y-x\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+3\left(x-y\right)+\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y+3+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-y=0\\x+y+4=0\end{cases}}\)
TH1 : x - y = 0 <=> x = y ta có : \(x^2-3x=x\) \(\Leftrightarrow x\left(x-4\right)=0\Leftrightarrow\orbr{\begin{cases}x=0=y\\x=4=y\end{cases}}\)
TH2 : x + y + 4 = 0 <=> y = -4-x ta có : \(x^2-3x=-x-4\)
\(\Leftrightarrow x^2-2x+4=0\)
\(\Leftrightarrow\left(x-1\right)^2+3=0\left(vonghiem\right)\)
12. \(\hept{\begin{cases}x^3+x^2y=10y\\y^3+xy^2=10x\end{cases}}\)
\(\Leftrightarrow x^3-y^3+x^2y-xy^2=10y-10x\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)+10\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+2xy+y^2+10\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[\left(x+y\right)^2+10\right]=0\)
mà có \(\left(x+y\right)^2+10>0\)
\(\Rightarrow x-y=0\Leftrightarrow x=y\)
ta có : \(x^3+x^3=10x\)
\(\Leftrightarrow2x^3-10x=0\Leftrightarrow2x\left(x^2-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0=y\\x=\pm\sqrt{5}=y\end{cases}}\)
mấy cái hệ đối xứng này lấy pt trên trừ dưới là ra thôi, thể nào cũng có nghiệm x=y

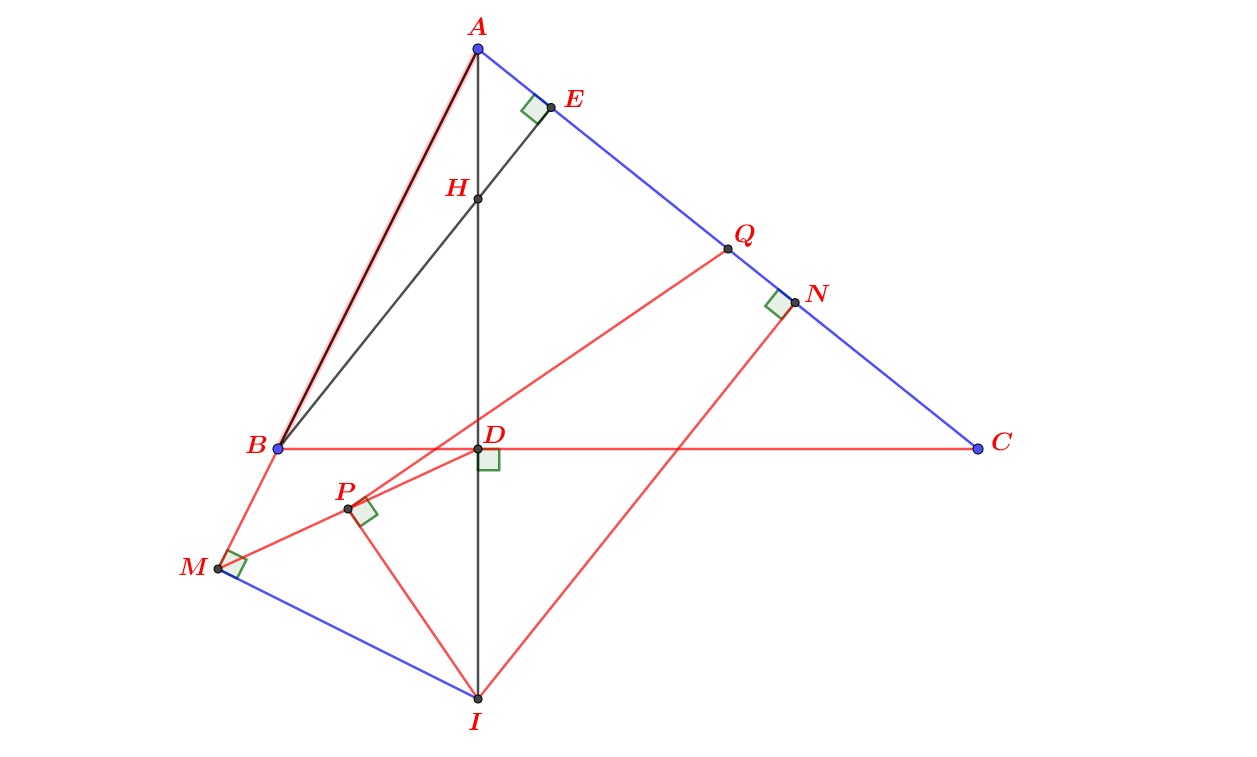
a.Vì P,H đối xứng qua AM, H, Q đối xứng qua MB
→HI⊥AM,HJ⊥MB→HI⊥AM,HJ⊥MB
Mà AM⊥MB→MIHJAM⊥MB→MIHJ là hình chữ nhật
→→bốn điểm M , I , H , J thuộc một đường tròn.
b.Ta có : HI⊥AM,MH⊥AB,HJ⊥MB→MI.MA=MH2=MJ.MBHI⊥AM,MH⊥AB,HJ⊥MB→MI.MA=MH2=MJ.MB
c.Vì P,HP,H đối xứng qua AM
→ˆPMA=ˆAMH=ˆMBA→PM→PMA^=AMH^=MBA^→PM là tiếp tuyến của (O)
Tương tự MQMQ là tiếp tuyến của (O)
→PQ→PQ là tiếp tuyến của (O)
d.Ta có :
BKKP=BQAP=BHAH=BJJM→KJ//MPBKKP=BQAP=BHAH=BJJM→KJ//MP
Tương tự KI//MQ→I,K,JKI//MQ→I,K,J thẳng hàng

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp

Nhận xét: với mọi n nguyên thì \(n^2\equiv\left\{0;1;2;4\right\}\left(mod7\right)\)
Giả sử a;b tồn tại 1 số không chia hết cho 7
\(\Rightarrow a^2+b^2\equiv\left\{1;2;3;4;5;6;8\right\}\left(mod7\right)\)
\(\Rightarrow a^2+b^2\) luôn ko chia hết cho 7 (trái với giả thiết)
Vậy điều giả sử là sai hay \(a;b\) đều chia hết cho 7

 em nhờ các thầy cô gợi ý lời giải bài 17 và 18 giúp em ạ
em nhờ các thầy cô gợi ý lời giải bài 17 và 18 giúp em ạ

