DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TG
3
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
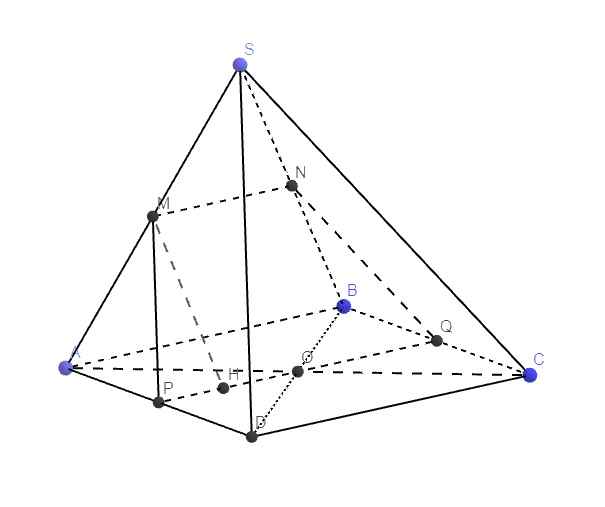
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
S
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2021
Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị
DT
1
15 tháng 6 2023
38:
a: (SAB) và (SAC) cùng vuông góc (ABC)
(SAB) cắt (SAC)=SA
=>SA vuông góc (ABC)
b: SA vuông góc CH
CH vuông góc AB
=>CH vuông góc (SAB)
=>(SCH) vuông góc (SAB)
MT
2
26 tháng 8 2021
Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
TT
20 tháng 8 2021
Câu 1: ĐK: \(x\ne k\pi\)
\(3cotx-\sqrt{3}=0\) \(\Leftrightarrow cotx=\dfrac{\sqrt{3}}{3}\) \(\Leftrightarrow x=\dfrac{1}{3}\pi+k\pi\)
Chọn B
Câu 2: D
AW
4
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
3.
\(u_2=\dfrac{1}{2-u_1}=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)
\(u_3=\dfrac{1}{2-u_2}=\dfrac{1}{2-\dfrac{2}{3}}=\dfrac{3}{4}\)
\(u_4=\dfrac{1}{2-\dfrac{3}{4}}=\dfrac{4}{5}\)
4.
\(u_1=\dfrac{2^{1+1}+1}{2^1}=\dfrac{5}{2}\)
\(u_3=\dfrac{2^4+1}{2^3}=\dfrac{17}{8}\)
\(u_5=\dfrac{2^6+1}{2^5}=\dfrac{65}{32}\)
5. Đề bị khuất
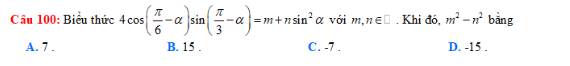
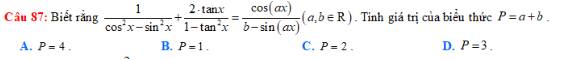
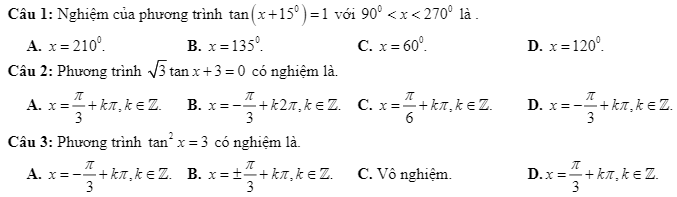
Bạn muốn gì?