K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
17 tháng 9 2023
Lời giải:
a. ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\frac{x+\sqrt{x}}{\sqrt{x}+2}\)
\(=\frac{x+\sqrt{x}+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{x}{\sqrt{x}-1}\)
b.
$P>2 \Leftrightarrow \frac{x}{\sqrt{x}-1}-2>0$
$\Leftrightarrow \frac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0$
$\Leftrightarrow \frac{(\sqrt{x}-1)^2+1}{\sqrt{x}-1}>0$
$\Leftrightarrow \sqrt{x}-1>0$ (do $(\sqrt{x}-1)^2+1>0$)
$\Leftrightarrow x>1$
Kết hợp đkxđ suy ra $x>1$
c.
$\frac{1}{P}=\frac{\sqrt{x}-1}{x}$
Áp dụng BĐT Cô-si:
$x+4\geq 4\sqrt{x}\Rightarrow x\geq 4(\sqrt{x}-1)$
$\Rightarrow \frac{\sqrt{x}-1}{x}\leq \frac{\sqrt{x}-1}{4(\sqrt{x}-1)}=\frac{1}{4}$
Vậy $\frac{1}{P}$ max $=\frac{1}{4}$ khi $x=4$
14 tháng 10 2023
a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=30^0\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{4}{BC}=sin30=\dfrac{1}{2}\)
=>BC=8(cm)
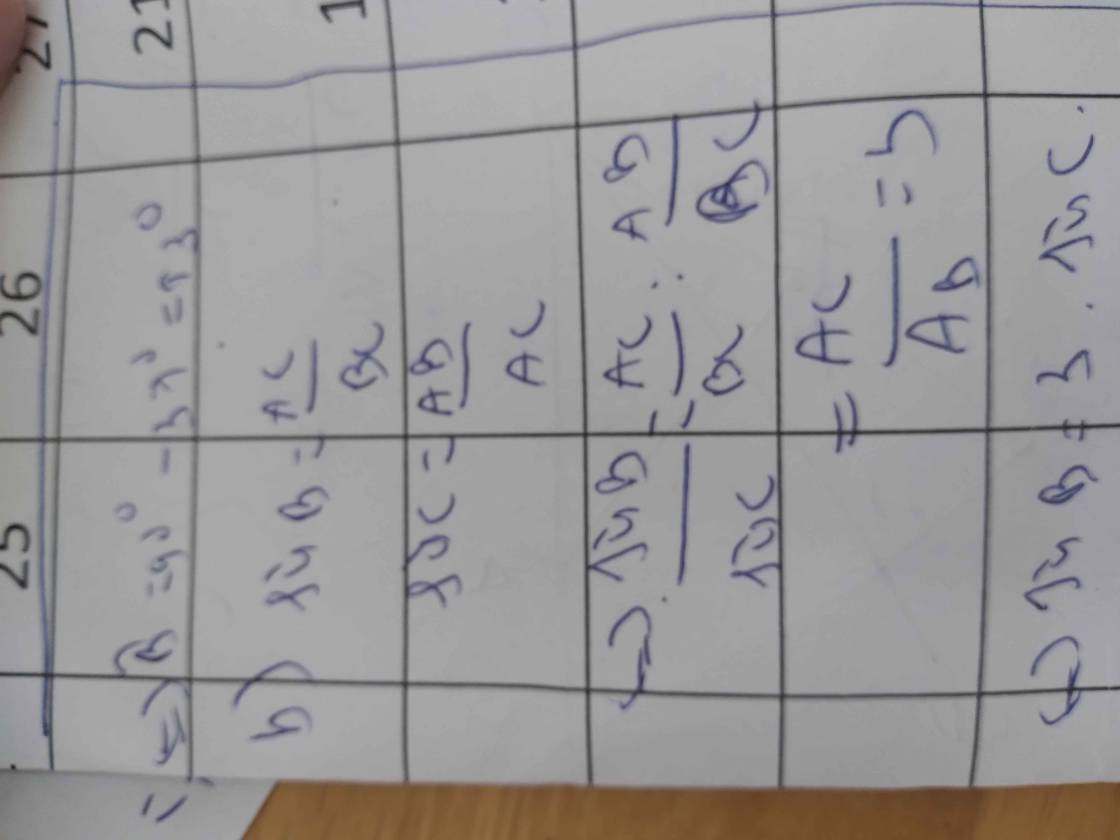
\(AC=\sqrt{BC^2-AB^2}=4\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>\(AH\cdot8=4\cdot4\sqrt{3}=16\sqrt{3}\)
=>\(AH=2\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{4^2}{8}=2\left(cm\right)\\CH=\dfrac{48}{8}=6\left(cm\right)\end{matrix}\right.\)
b: \(BC\cdot sinB\cdot sinC\)
\(=BC\cdot\dfrac{AC}{BC}\cdot\dfrac{AB}{BC}=\dfrac{AB\cdot AC}{BC}=AH\)
\(BC\cdot cos^2B\)
\(=BC\cdot\left(\dfrac{AB}{BC}\right)^2=\dfrac{AB^2}{BC}=BH\)
\(BC\cdot sin^2B=BC\cdot\left(\dfrac{AC}{BC}\right)^2=\dfrac{AC^2}{BC}=CH\)
c:
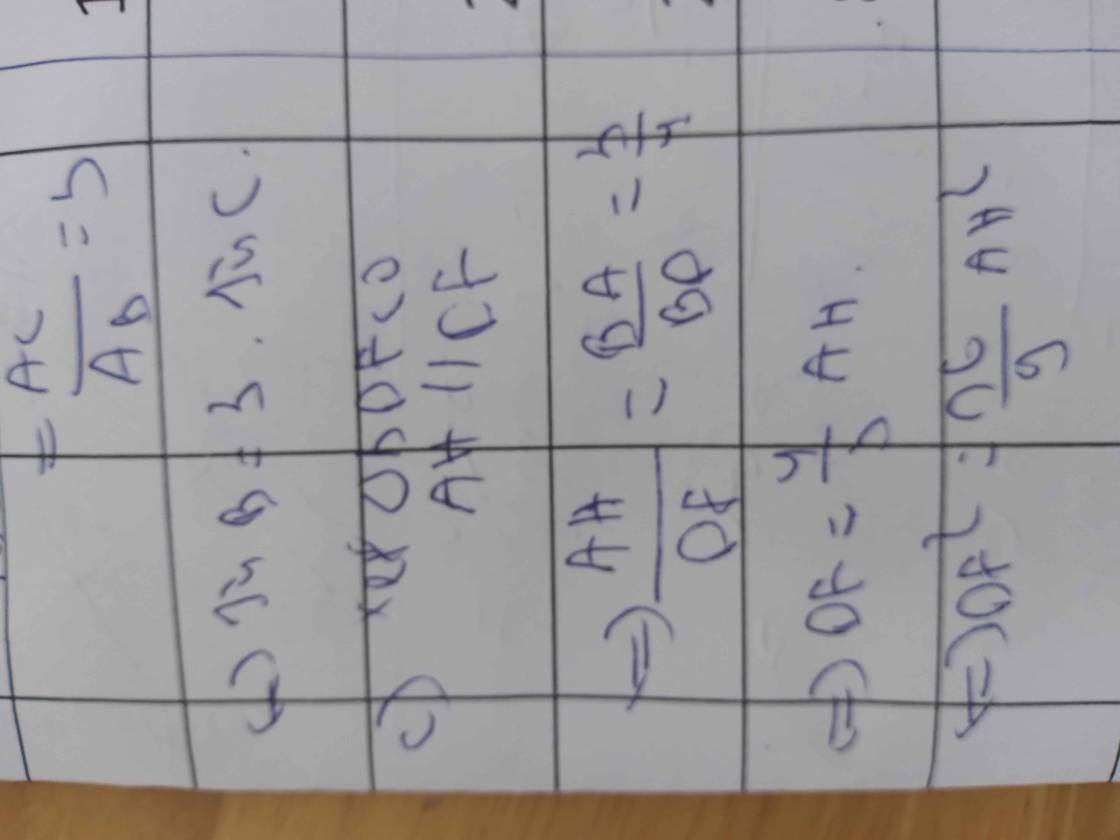
\(\dfrac{AH^2}{AC^2}=\dfrac{HB\cdot HC}{BC\cdot HC}=\dfrac{HB}{BC}\)
ΔHAB vuông tại H có HD là đường cao
nên \(\left\{{}\begin{matrix}BD\cdot BA=BH^2\\AD\cdot AB=AH^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=\dfrac{BH^2}{AB}\\AD=\dfrac{AH^2}{AB}\end{matrix}\right.\)
ΔHAC vuông tại H có HE là đường cao
nên \(\left\{{}\begin{matrix}CE\cdot CA=CH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}CE=\dfrac{CH^2}{AC}\\AE=\dfrac{AH^2}{AC}\end{matrix}\right.\)
\(\dfrac{DB}{EC}=\dfrac{HB^2}{AB}:\dfrac{HC^2}{AC}\)
\(=\dfrac{HB^2}{AB}\cdot\dfrac{AC}{HC^2}\)
\(=\left(\dfrac{HB}{HC}\right)^2\cdot\dfrac{AC}{AB}=\dfrac{AC}{AB}\cdot\left(\dfrac{AB}{AC}\right)^4=\left(\dfrac{AB}{AC}\right)^3\)
\(BD\cdot CE\cdot BC\)
\(=\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\cdot BC\)
\(=\dfrac{AH^4}{AH}=AH^3\)
=DE3
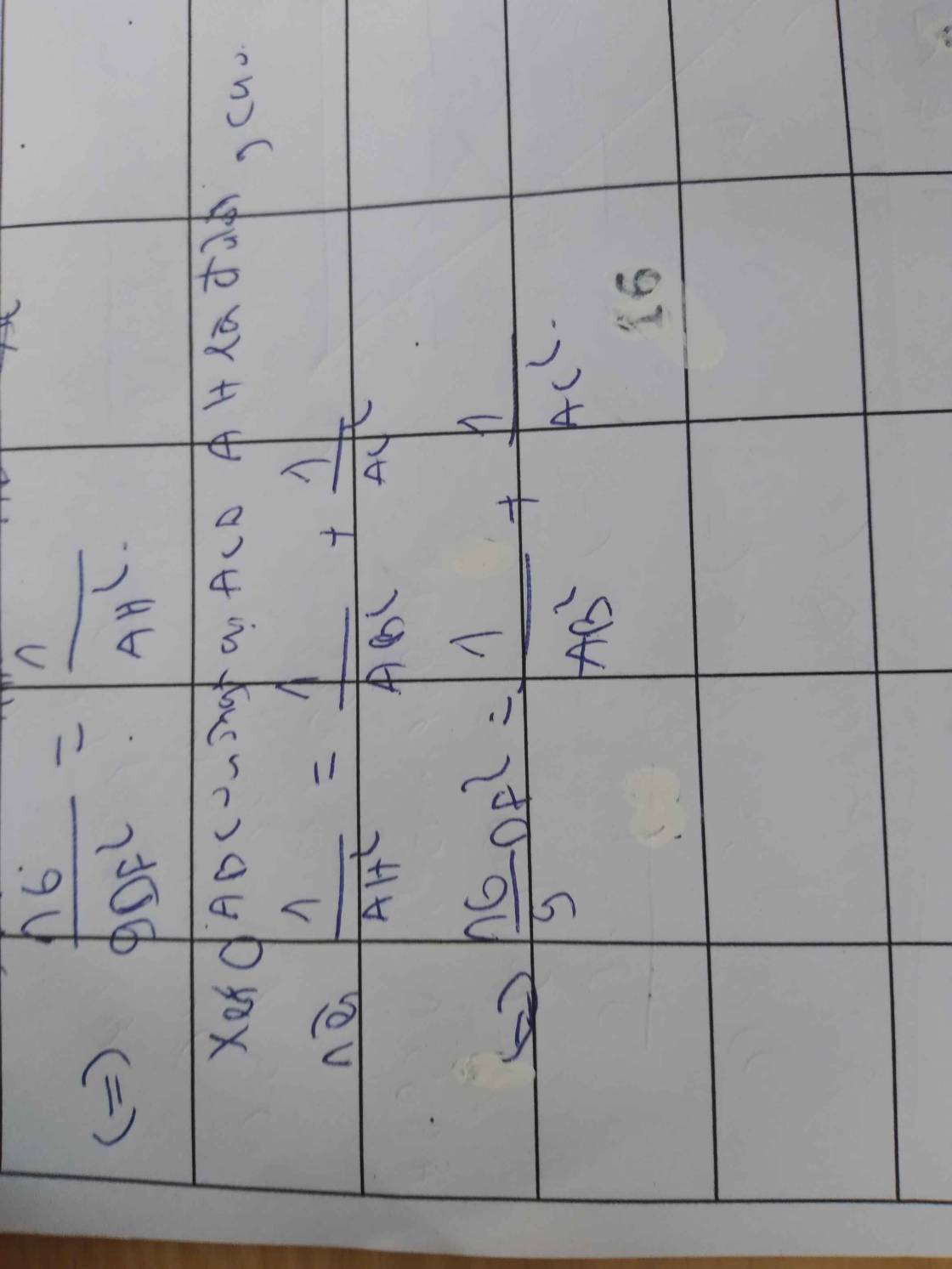
\(BC\cdot HD\cdot HE\)
\(=BC\cdot\dfrac{HA\cdot HB}{AB}\cdot\dfrac{HA\cdot HC}{AC}\)
\(=\dfrac{1}{AH}\cdot\dfrac{HA^2\cdot HB\cdot HC}{1}=\dfrac{HA\cdot HB\cdot HC}{1}=HA^3\)
\(=DE^3\)
=>ĐPCM
22 tháng 11 2023
Bài 2:
a: (d)//y=-2x+3 nên \(\left\{{}\begin{matrix}a=-2\\b\ne3\end{matrix}\right.\)
vậy: (d): y=-2x+b
Thay x=-1 và y=1 vào (d), ta được:
\(b+\left(-2\right)\cdot\left(-1\right)=1\)
=>b+2=1
=>b=-1
Vậy: (d): y=-2x-1
b: Thay x=0 và y=1 vào (d), ta được:
\(0\cdot a+b=1\)
=>b+0=1
=>b=1
Vậy: (d): y=ax+1
Thay x=-3 và y=0 vào (d), ta được:
\(-3\cdot a+1=0\)
=>-3a=-1
=>\(a=\dfrac{1}{3}\)
Vậy: (d): \(y=\dfrac{1}{3}x+1\)
Bài 1:
a: Vì (d)//y=-3x+1 nên a=-3 và b<>1
vậy: (d): y=-3x+b
Thay x=1/3 và y=-1 vào (d), ta được:
\(b-3\cdot\dfrac{1}{3}=-1\)
=>b-1=-1
=>b=0
vậy: (d): y=-3x
b: Thay x=2 và y=0 vào (d), ta được:
\(a\cdot2+b=0\)
=>2a+b=0(1)
Thay x=-1 và y=4 vào (d), ta được:
\(a\cdot\left(-1\right)+b=4\)
=>-a+b=4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-4\\2a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-\dfrac{4}{3}\\b=-2a=-2\cdot\dfrac{-4}{3}=\dfrac{8}{3}\end{matrix}\right.\)
Vậy: (d): \(y=-\dfrac{4}{3}x+\dfrac{8}{3}\)
1 tháng 12 2023
3: Gọi giao điểm của CO với OB là H
Xét ΔOAC vuông tại A và ΔOBH vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOH}\)
Do đó: ΔOAC=ΔOBH
=>\(\widehat{OCA}=\widehat{OHB}\) và OC=OH
OC=OH
C,O,H thẳng hàng
Do đó: O là trung điểm của CH
Xét ΔDCH có
DO là đường cao
DO là đường trung tuyến
Do đó:ΔDCH cân tại D
ΔDCH cân tại D
mà DO là đường cao
nên DO là phân giác của góc CDH
ΔDCH cân tại D
=>\(\widehat{DCH}=\widehat{DHC}\)
mà \(\widehat{DHC}=\widehat{ACH}\)
nên \(\widehat{DCH}=\widehat{ACH}\)
=>CH là phân giác của góc ACD
Kẻ OK\(\perp\)CD tại K
Xét ΔCAO vuông tại A và ΔCKO vuông tại K có
CO chung
\(\widehat{ACO}=\widehat{KCO}\)
Do đó: ΔCAO=ΔCKO
=>OA=OK=R
Xét (O) có
OK là bán kính
CD\(\perp\)OK tại K
Do đó: CD là tiếp tuyến của (O)
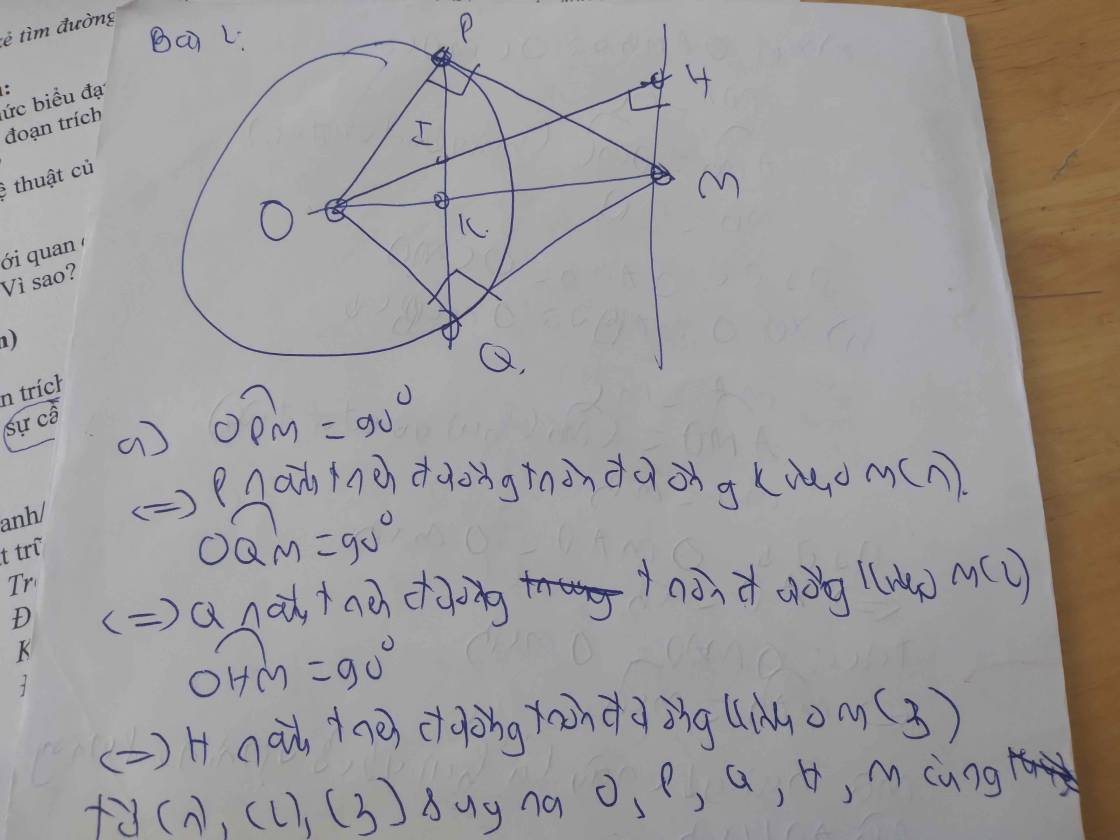
2:
ΔOAB cân tại O
mà OM là đường cao
nênOM là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
AH
Akai Haruma
Giáo viên
11 tháng 12 2023
b.
PT (1) $\Leftrightarrow (x+y)^2-2xy-3(x+y)=16(*)$
PT (2) $\Leftrightarrow xy=-7-(x+y)$. Thay vào $(*)$ thì:
$(x+y)^2-2[-7-(x+y)]-3(x+y)=16$
$\Leftrightarrow (x+y)^2+14-(x+y)=16$
$\Leftrightarrow (x+y)^2-(x+y)-2=0$
$\Leftrightarrow (x+y)^2+(x+y)-2(x+y)-2=0$
$\Leftrightarrow (x+y)(x+y+1)-2(x+y+1)=0$
$\Leftrightarrow (x+y+1)(x+y-2)=0$
$\Leftrightarrow x+y=-1$ hoặc $x+y=2$
Nếu $x+y=-1$ thì $xy=-7-(x+y)=-7-(-1)=-6$. Theo định lý Viet đảo thì $x,y$ là nghiệm của pt $X^2+X-6=0$
$\Rightarrow (x,y)=(2, -3), (-3,2)$
Nếu $x+y=2$ thì $xy=-7-(x+y)=-9$. Theo định lý Viet đảo thì $x,y$ là nghiệm của pt $X^2-2X-9=0$
$\Rightarrow (x,y)=(1+\sqrt{10}, 1-\sqrt{10}), (1-\sqrt{10}, 1+\sqrt{10})$
AH
Akai Haruma
Giáo viên
11 tháng 12 2023
c.
Lấy PT(1) trừ PT(2):
$x^2-y^2-(3x-3y)=y^2-x^2$
$\Leftrightarrow 2(x^2-y^2)-(3x-3y)=0$
$\Leftrightarrow (x-y)(2x+2y-3)=0$
$\Leftrightarrow x-y=0$ hoặc $2x+2y-3=0$
Nếu $x-y=0\Rightarrow x=y$. Thay vào PT(1):
$x^2-3x=x^2+1\Leftrightarrow x=\frac{-1}{3}\Rightarrow y=\frac{-1}{3]$
Nếu $2x+2y-3=0\Leftrightarrow y=\frac{3-2x}{2}$. Thay vào PT(1):
$x^2-3x=(\frac{3-2x}{2})^2+1$
$\Leftrightarrow x^2-3x=(1,5-x)^2+1=3,25+x^2-3x$
$\Leftrightarrow 3,25=0$ (vô lý - loại)
5 tháng 12 2023
a: \(\left\{{}\begin{matrix}x-2y+2=0\\2y-x^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2y=x+2\\2y=x^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2=x+2\\x^2=2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-x-2=0\\y=\dfrac{x^2}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\y=\dfrac{x^2}{2}\end{matrix}\right.\)
(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì \(y=\dfrac{x^2}{2}=\dfrac{2^2}{2}=\dfrac{4}{2}=2\)
Khi x=-1 thì \(y=\dfrac{x^2}{2}=\dfrac{\left(-1\right)^2}{2}=\dfrac{1}{2}\)
b: \(\left\{{}\begin{matrix}2x^2+xy+y^2-x=5\\4x^2+2xy+2y^2-y=4\end{matrix}\right.\)(I)
=>\(\left\{{}\begin{matrix}4x^2+2xy+2y^2-2x=10\\4x^2+2xy+2y^2-y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+y=6\\2x^2+xy+y^2-x=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+6\\2x^2+x\left(2x+6\right)+\left(2x+6\right)^2-x=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+6\\2x^2+2x^2+6x+4x^2+24x+36-x=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+6\\8x^2+29x+31=0\end{matrix}\right.\)
\(8x^2+29x+31=0\)(1)
\(\text{Δ}=29^2-4\cdot8\cdot31\)
\(=841-32\cdot31=-151< 0\)
=>Phương trình (1) vô nghiệm
Do đó: Hệ phương trình (I) vô nghiệm
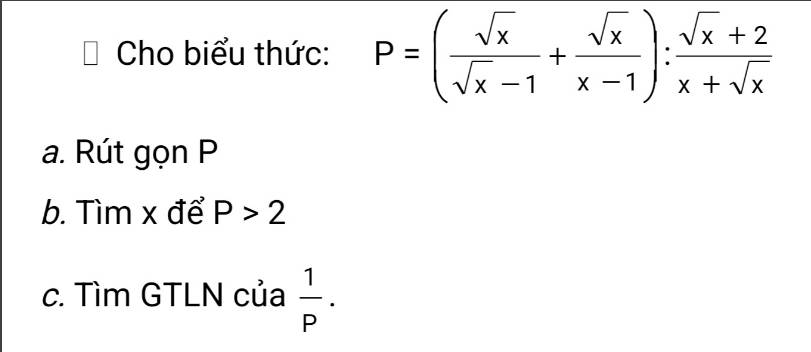
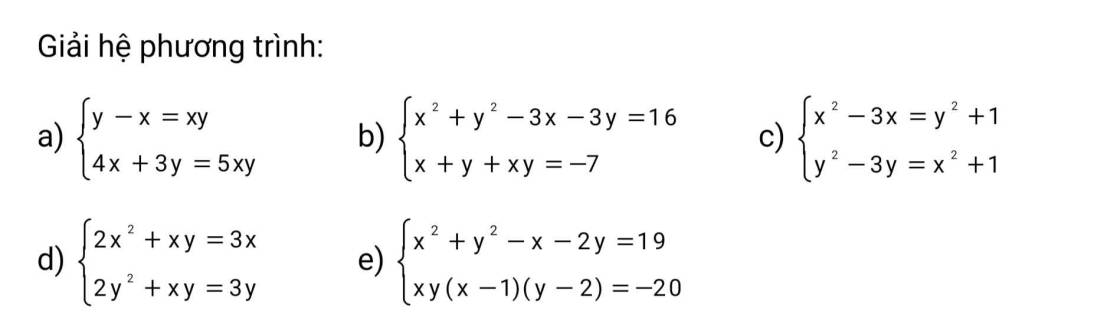
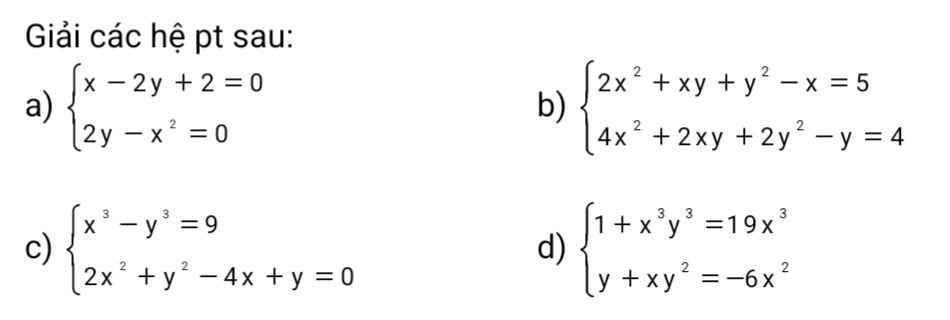
Bài 1:
a: Ta có: AH\(\perp\)BM
OB\(\perp\)BM
Do đó: AH//OB
Ta có: BH\(\perp\)AM
OA\(\perp\)AM
Do đó: BH//OA
Xét tứ giác OAHB có
OA//HB
OB//HA
Do đó: OAHB là hình bình hành
Hình bình hành OAHB có OA=OB
nên OAHB là hình thoi
b: Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=2\cdot30^0=60^0\)
Bài 2:
a: Xét tứ giác CAOD có
\(\widehat{CAO}+\widehat{CDO}=90^0+90^0=180^0\)
=>CAOD là tứ giác nội tiếp
=>C,A,O,D cùng thuộc một đường tròn
b: Ta có: ΔCAO vuông tại A
=>\(CO^2=CA^2+AO^2\)
=>\(CO^2=\left(2R\right)^2+R^2=5R^2\)
=>\(CO=R\sqrt{5}\)
Xét ΔCAO vuông tại A có AH là đường cao
nên \(AH\cdot CO=AO\cdot AC\)
=>\(AH\cdot R\sqrt{5}=R\cdot2R=2R^2\)
=>\(AH=\dfrac{2R^2}{R\sqrt{5}}=\dfrac{2R}{\sqrt{5}}\)
Xét (O) có
CA,CD là tiếp tuyến
Do đó: CA=CD
=>C nằm trên đường trung trực của AD(1)
ta có: OA=OD
=>O nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra OC là đường trung trực của AD
=>OC\(\perp\)AD tại H và H là trung điểm của AD
=>\(AD=2\cdot AH=\dfrac{4R}{\sqrt{5}}\)