
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng

a) Dùng 

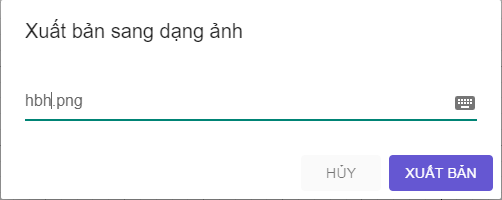
b) Lưu hình vẽ ở HĐ2 thành tệp hbh.png.
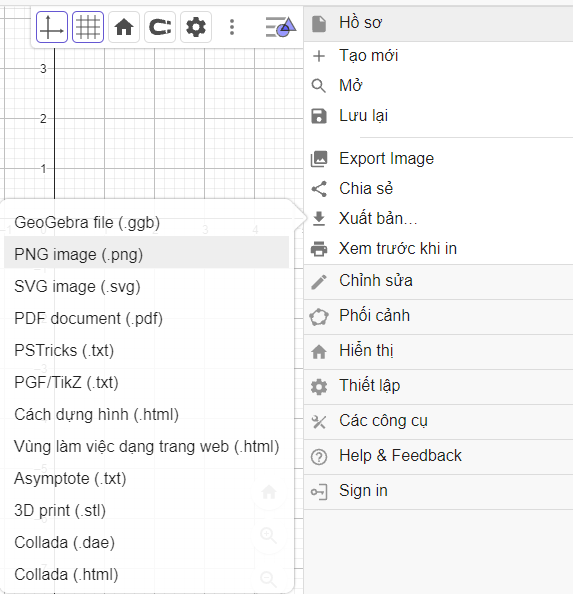
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
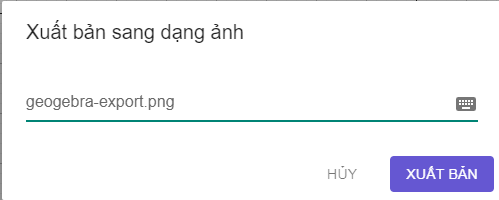
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
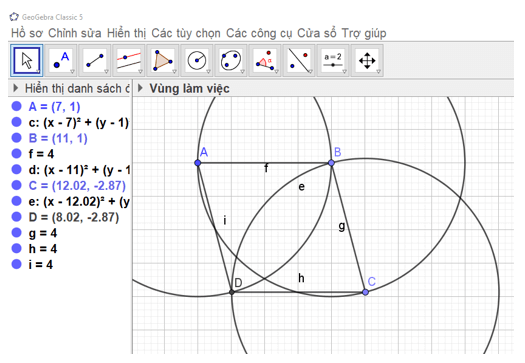
Bước 1. Vẽ đoạn thẳng AB và có độ dài 4 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ điểm C sao cho BC = 4 cm.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 
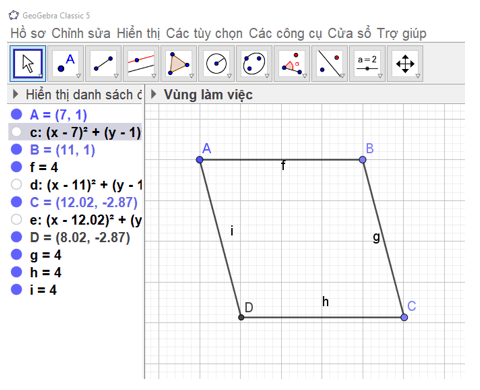
Bước 3. Ẩn đường tròn và thu được hình thoi ABCD.

Ta có
\(BC\perp AB';B'C'\perp AB'\) => BC//B'C'
\(\Rightarrow\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\Rightarrow\dfrac{x}{x+h}=\dfrac{a}{a'}\)
\(\Rightarrow a'x=ax+ah\Rightarrow x\left(a'-a\right)=ah\Rightarrow x=\dfrac{ah}{a'-a}\left(dpcm\right)\)
Xét tam giác ABCABC có BC⊥ AB′BC⊥ AB′ và B′C′⊥AB′B′C′⊥AB′ nên suy ra BCBC // B′C′B′C′.
Theo hệ quả định lí Thalès, ta có: ABAB′ =BCBC′AB′AB =BC′BC
Suy ra xx+h =aa′x+hx =a′a
a′.x=a(x+h)a′.x=a(x+h)
a′.x−ax=aha′.x−ax=ah
x(a′−a)=ahx(a′−a)=ah
x=aha′ −ax=a′ −aah.

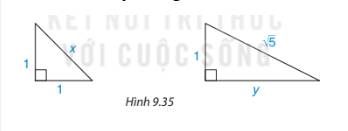
\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
a) \(x^2=1^2+1^2=2\Rightarrow x=\sqrt[]{2}\)
b) \(\left(\sqrt[]{5}\right)^2=y^2+1^2\Rightarrow y^2=5-1=4\Rightarrow y=2\)

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

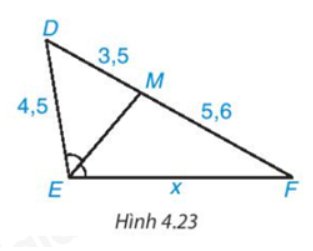
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).
 nhanh mọi người ơi đang cần rất rất gấp luôn á
nhanh mọi người ơi đang cần rất rất gấp luôn á 




 trong công cụ
trong công cụ  để kiểm tra trung điểm AC và BD có trùng nhau không.
để kiểm tra trung điểm AC và BD có trùng nhau không.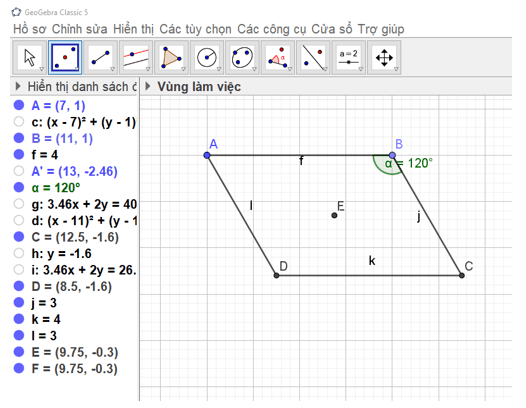


quá là gấp r ạ phiền mn nhanh nhanh giúp em ạ