
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Pha của li độ và gia tốc của một dao động cùng pha với nhau

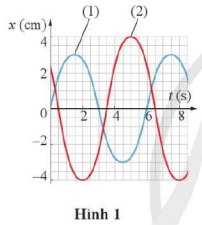
a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)

a) Hình dạng đồ thị gia tốc – thời gian của vật là dạng hình sin.
b) Chu kì của gia tốc của vật là T=0,66 s.
c) Mối liên hệ giữa gia tốc cực đại và biên độ của vật là khi gia tốc đạt giá trị cực đại khi ở vị trí biên và cực tiểu khi ở vị trí cân bằng.
d) Độ lệch pha của gia tốc so với li độ của vật là π.

a) Hình dạng đồ thị vận tốc – thời gian của vật là dạng hình sin.
b) Chu kì của vận tốc của vật T=0,66 s.
c) Mối liên hệ giữa tốc độ cực đại và biên độ của vật: khi vận tốc cực đại thì biên độ cực tiểu và ngược lại.
d) Độ lệch pha của vận tốc so với li độ của vật là \(\dfrac{\pi}{2}\)

Phương trình: \(x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
a)Biên độ: \(A=2cm\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
Chiều dài quỹ đạo: \(L=2A=2\cdot2=4cm\)
b)Phương trình chất điểm:
Vận tốc: \(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)\)
Gia tốc: \(a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
c)Em thay giá trị \(t=0,2s\) vào từng pt nhé.

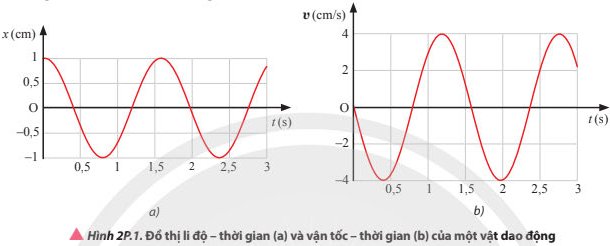
Từ đồ thị ta xác định được A = 1cm
Ta có: vmax = ωA⇒ω = 4 (rad/s)
Phương trình li độ của dao động: x = cos(4t) (cm)
Phương trình vận tốc của dao động: v = 4cos(4t+\(\frac{\pi }{2}\)) (cm/s)
Phương trình gia tốc của vật dao động: a = 16cos(4t) (m/s2)

Phương trình vận tốc:
\(v=-4\pi\cdot5sin4\pi t=20\pi cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm/s\right)\)
Phương trình gia tốc:
\(a=-\omega^2x=-\left(4\pi\right)^2\cdot5cos4\pi t=80\pi^2cos\left(4\pi t+\pi\right)\left(cm/s^2\right)\)

Giả sử pt dao động của vật có dạng:
\(x=Acos\left(5t+\varphi\right)\left(cm\right)\)
\(\Rightarrow v=-5Asin\left(5t+\varphi\right)=5Acos\left(\dfrac{\pi}{2}+5t+\varphi\right)\left(\text{cm/s}\right)\)
Tại \(t=0:\)\(\left\{{}\begin{matrix}x=-2\left(cm\right)\\v=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=Acos\varphi=-2\left(cm\right)\\v_0=5Acos\left(\dfrac{\pi}{2}+\varphi\right)=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=-\dfrac{2}{A}\left(1\right)\\5A\left(cos\dfrac{\pi}{2}.cos\varphi-sin\dfrac{\pi}{2}.sin\varphi\right)=10\end{matrix}\right.\)
\(\Rightarrow5A.\left(-sin\varphi\right)=10\Leftrightarrow sin\varphi=\dfrac{-2}{A}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\varphi=\dfrac{-3\pi}{4}\left(rad\right);A=2\sqrt{2}\left(cm\right)\)
Vậy ta có ptdđ của vật: \(x=2\sqrt{2}cos\left(5t-\dfrac{3\pi}{4}\right)\left(cm\right)\)
b)\(v_{max}=\omega A=5A=10\sqrt{2}\left(\text{cm/s}\right)\)
\(a_{max}=\omega^2A=50\sqrt{2}\left(\text{cm/s}^2\right)\)
c) \(\alpha=\Delta t.\omega=1,4\pi.5=7\pi\left(rad\right)=6\pi+\pi\left(rad\right)\)
\(\Rightarrow S=3.4A+2\sqrt{2}-2+2\sqrt{2}+2=12A+4\sqrt{2}=28\sqrt{2}\left(cm\right)\)
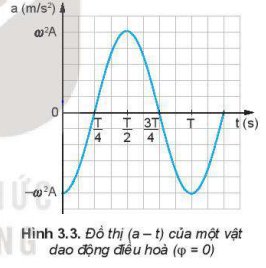
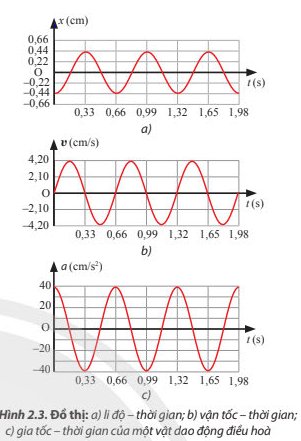
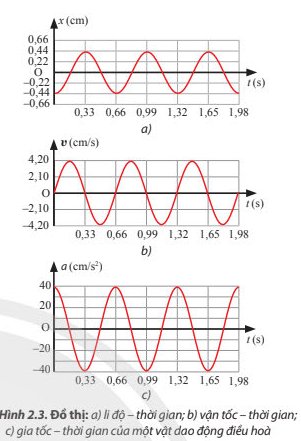

Độ lệch pha giữa gia tốc và vận tốc là \(\dfrac{\pi}{2}\).